Find Area

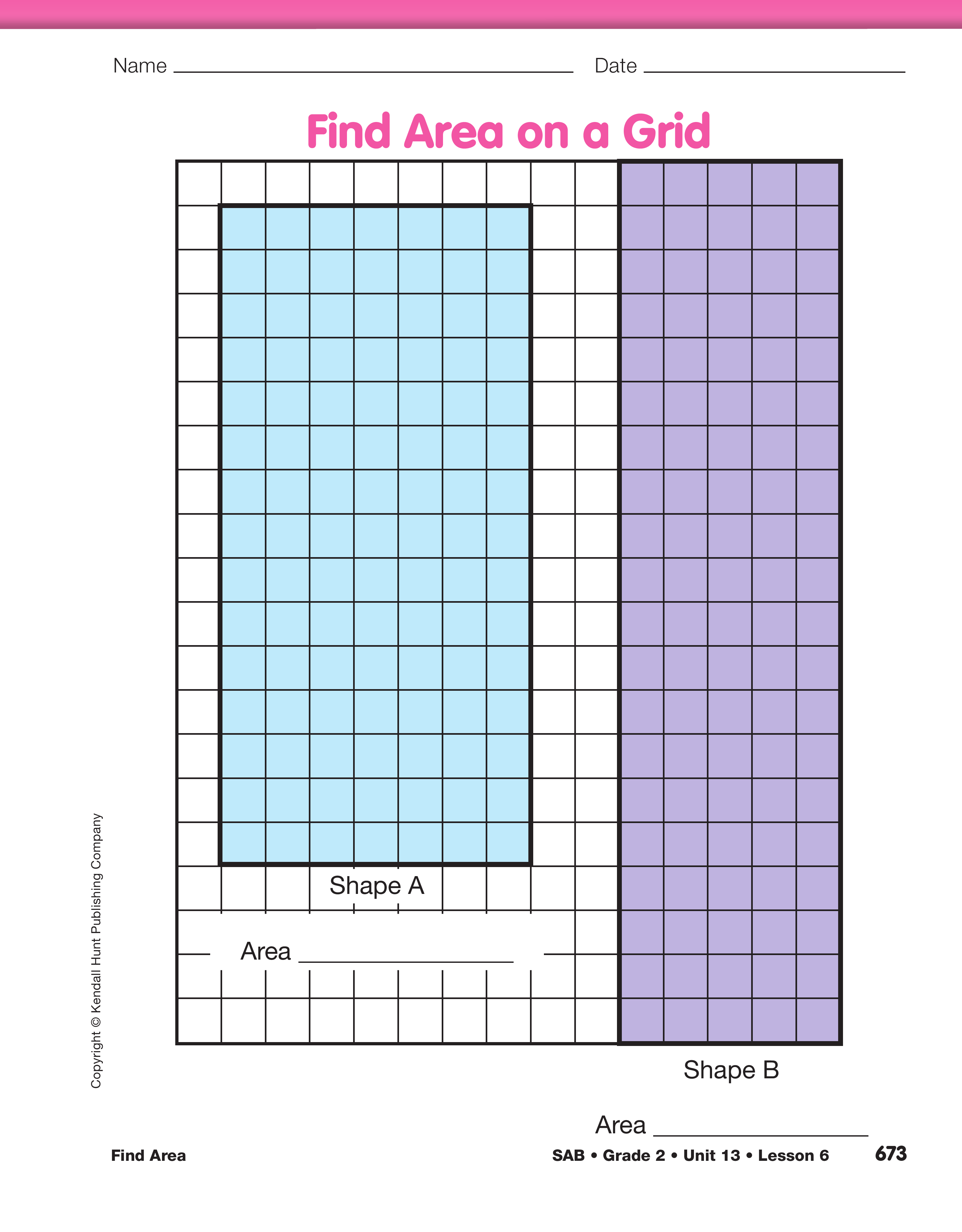
Count Square Units. Display and direct students' attention to the Find Area on a Grid pages in the Student Activity Book. Students will see Shape A and Shape B on a centimeter grid.

Tell students that these units are called square centimeters and are a common unit for measuring area of relatively small objects and surfaces.

Look for responses like the following:

• "We can use square centimeters in both shapes."
• "The square centimeters are easy to count, and the measurement is easy to report because they are all the same."
• "All the space is covered. There are no gaps or empty spaces."

Tell the class they are going to count the square centimeters in each shape. Remind students that they report the area using the appropriate unit, square centimeters.

Suggest that students count and number each square centimeter. Start the counting by writing the numbers across the first row of the rectangle on display.

Have a student demonstrate by counting square centimeters along the length and the width.

Give the students a few minutes to discuss with a partner possible ways to count more efficiently. The dimensions of this shape do not lend themselves to easy skip counting for second-graders. However, some students may suggest ways to make the counting more efficient. The point is to get students thinking of ways to count the arrays efficiently. Possible suggestions are:

• Draw a line at 10 rows and skip count those by tens; 10 rows of 7 is 70; then count the rest of the square centimeters by ones and add. 70 + 35 = 105 square centimeters. See Figure 6.
• Each column of 15 sq cm is the same as three 5s; mark three 5s in each column and skip count by fives, 3 times for each column. Skip counting by five twenty-one times comes to 105 square centimeters. See Figure 7.

If students do not suggest these or other methods of counting the square centimeters, suggest adding 7 repeatedly to get the total. See Figure 8.

Write 14 in the last space of the second row.

Compare with the answers found using other counting strategies.

Next, ask students to figure the area of Shape B. Students should see that they can skip count by 5s to find this area.

Have a student verify by counting the square centimeters in a row and a column. Have another student verify the measurements by measuring the sides using a centimeter ruler.

Have students skip count to find the area.

Label each shape with its area, including the unit. Shape A is 105 square centimeters and Shape B is 100 square centimeters.

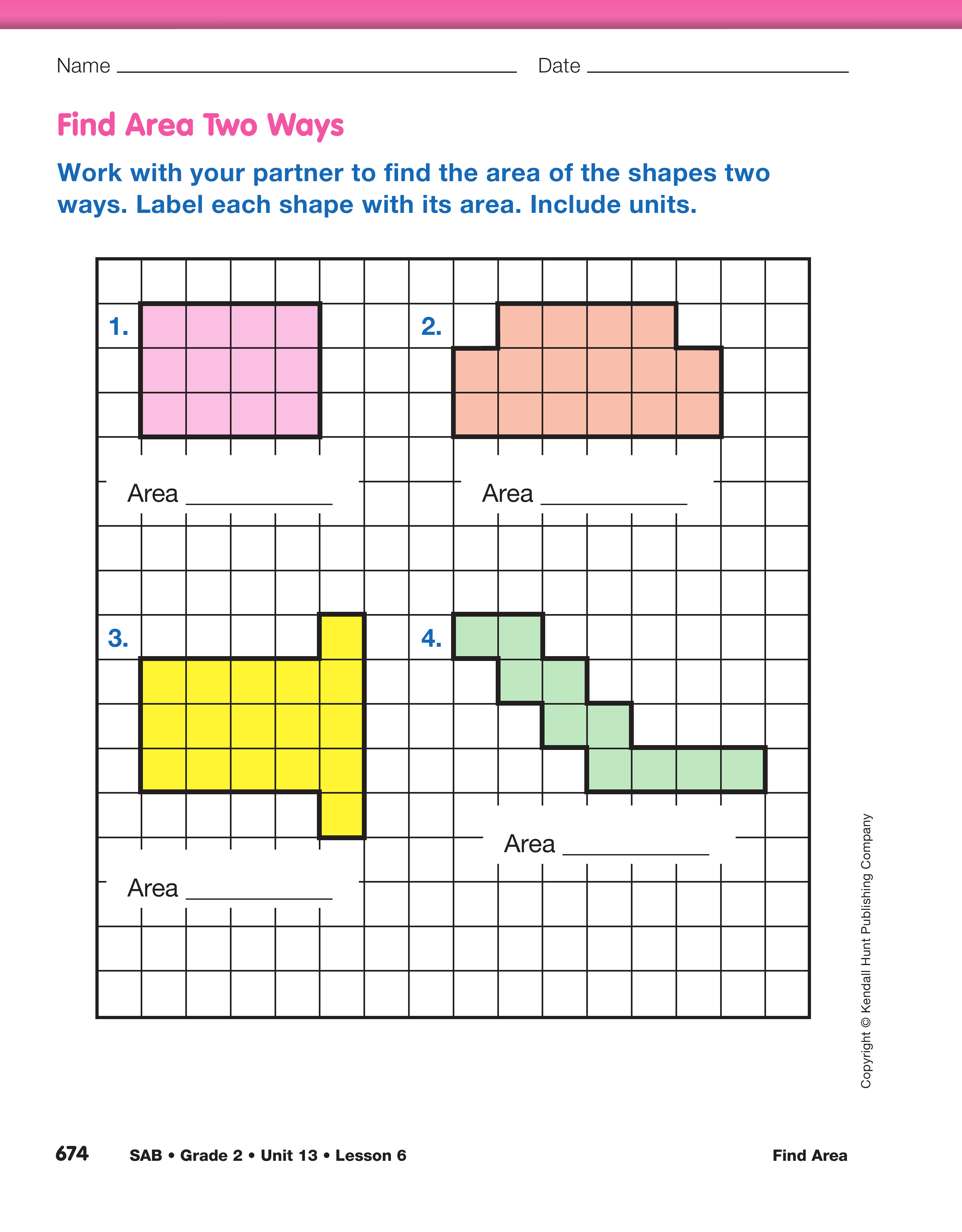
Find Area Two Ways. Direct students to the Find Area Two Ways section of the Find Area on a Grid pages in the Student Activity Book.

Assign Questions 1–4 to student pairs. Ask students to find two ways to find the area of each shape so that they can check the reasonableness of their answers. Encourage students to use strategies such as counting, skip counting, repeated addition, reasoning, decomposing the shape into rectangles, or multiplication if they are ready to do so. For example, for Question 1, students may first skip count the columns by threes (3, 6, 9, 12) and then multiply 3 × 4 to verify an area of 12 square centimeters. Remind students to label each shape with its area including the unit. Tell them they can use sq cm as an abbreviation of square centimeter. Circulate as students work and select a few to explain their solution strategies. Try to select a variety of strategies.

Upon completion, display the second Find Area on a Grid page and have selected students explain the strategies they used to find the areas of each of the shapes. Write the areas on the display including the units, square centimeters. See the Sample Dialog for sample questions.

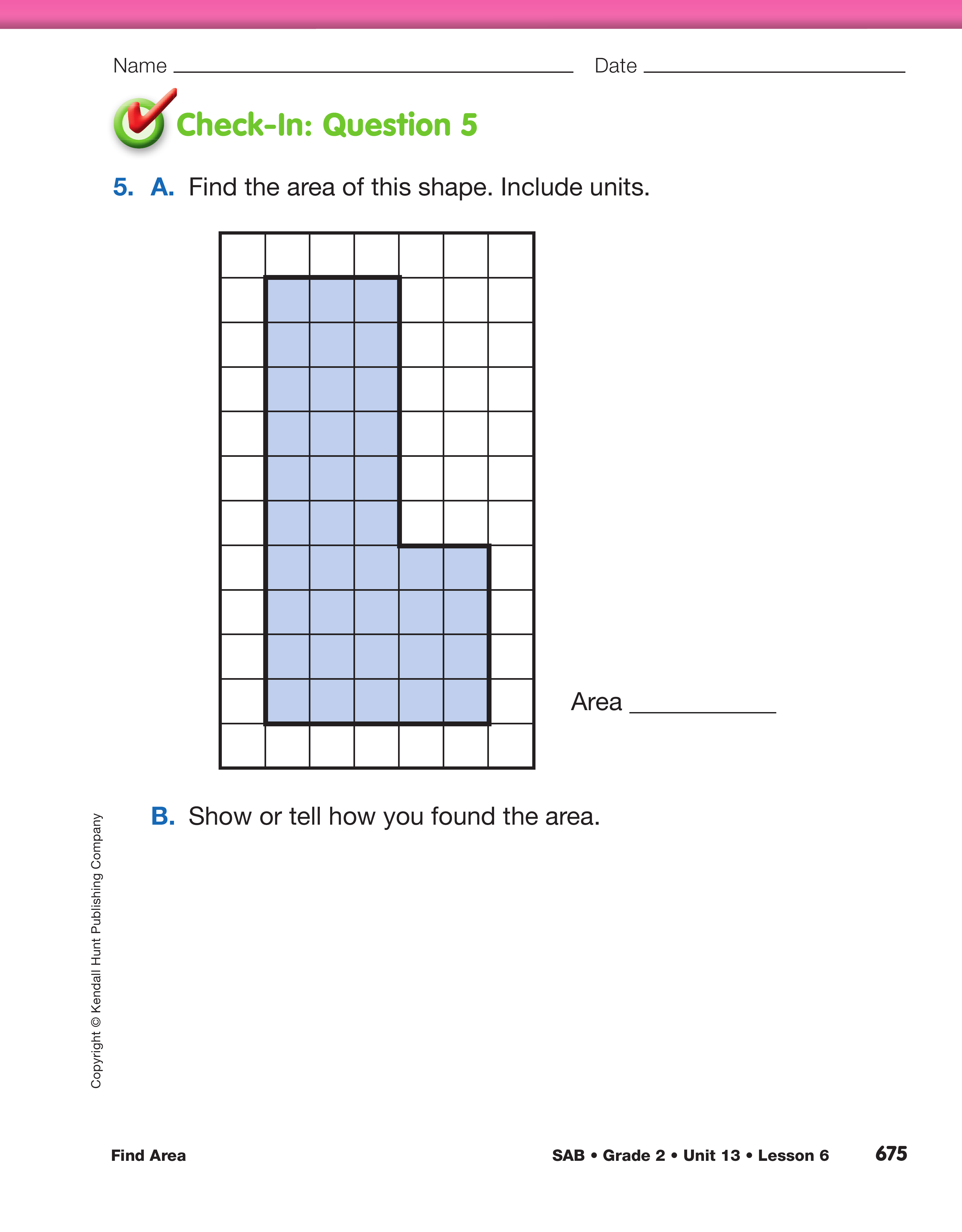
After some discussion, assign Check-In: Question 5 for students to complete individually.

Assign the Find Area at Home Homework Masters after Part 2 to provide more practice finding the area of a shape.