Area Riddles

Est. Class Sessions: 1

Developing the Lesson

Introduce Area Riddles. Display and direct students to the Area Riddles page in the Student Activity Book.

Ask:

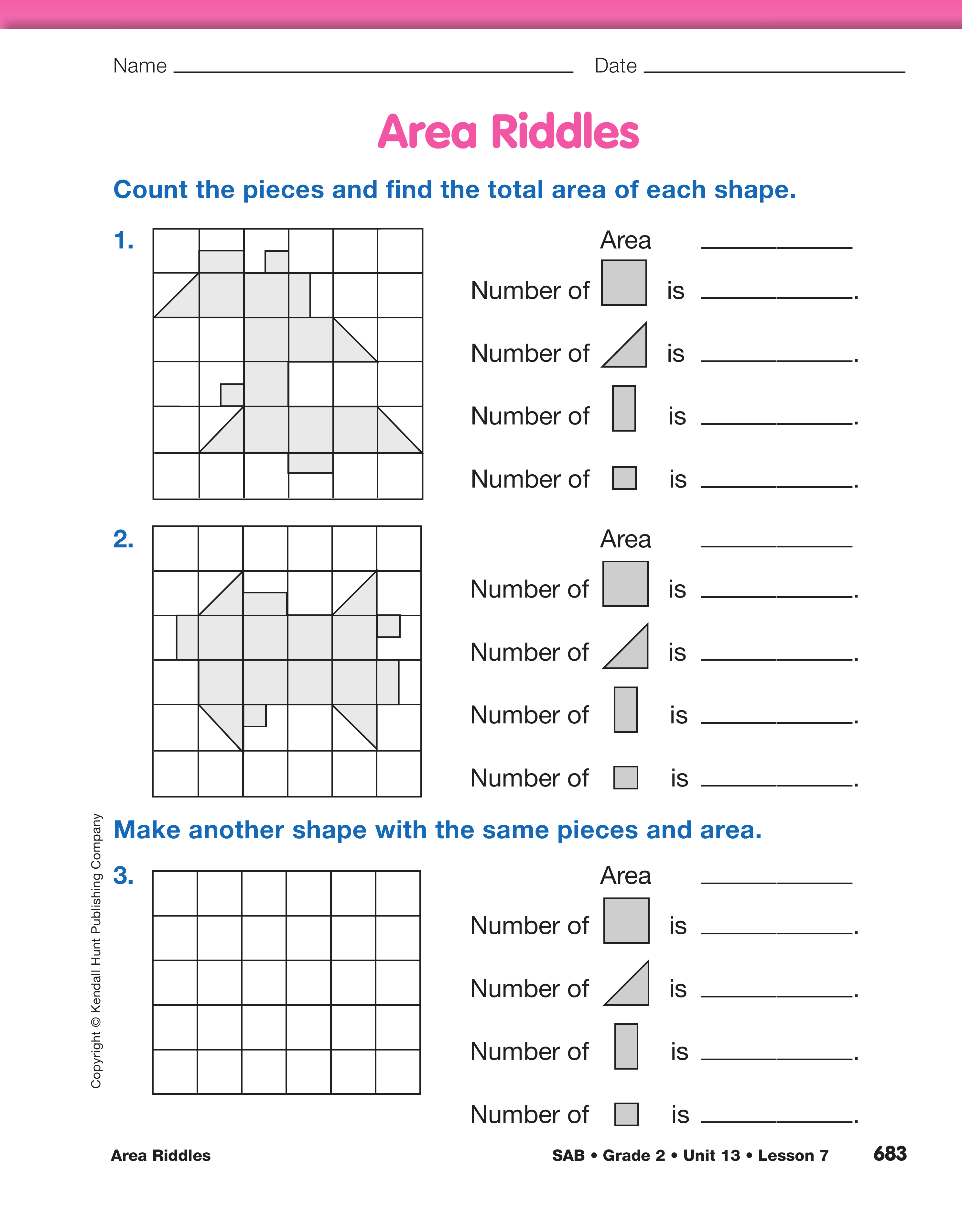
Describe how the two shapes in Questions 1 and 2 are alike and different. (Possible response: The shapes look different but are made up of similar pieces like the whole square centimeters and half square centimeters.)

Select student volunteers to help count the pieces in the shapes and fill in the missing information in Questions 1 and 2 as all students follow along. Each shape has 8 square centimeters, 4 triangular halves, 3 rectangular halves, and 2 fourths. Once this information is tallied, have students work with a partner to find the area of each shape. Each shape has a total area of 12 square centimeters.

Referring to the display, ask:

Show us how you found the area of the shape in Question 1. (Possible response: There are 8 whole square centimeters and 7 halves. 7 halves make 3 more whole square centimeters with 1 half leftover. There are 2 fourths and that makes another half. I put the leftover half with the 2 fourths to make another whole square centimeter. 8 + 3 + half + two fourths = 8 + 3 + 1. That makes 12 square centimeters.)
Show us how you found the area of the shape in Question 2. (Possible response: There were two rows of 4 whole square centimeters. That makes 8 square centimeters. Then I put all the triangle halves together. That makes 2 whole square centimeters. Then I put all the rectangle halves together to make another whole. I had one half left over so I put it together with the two fourth pieces. That made another whole square centimeter. I added up all the whole square centimeters: 8 + 2 + 1 + 1 = 12 square centimeters.)
What do you notice about the two shapes? (They have the same area, but they look different.)
Can two different shapes have the same area? How do you know? (Yes; I can count the square centimeters in both shapes and they both have an area of 12 square centimeters.)

Encourage students to use the grid space in Question 3 to draw an additional shape with the same combination of pieces (8 square centimeters, 4 triangular halves, 3 rectangular halves, 2 fourths) and the same area (12 sq cm) as the shapes in the previous questions. Students should compare their shapes to reinforce the idea that different shapes can have the same area.

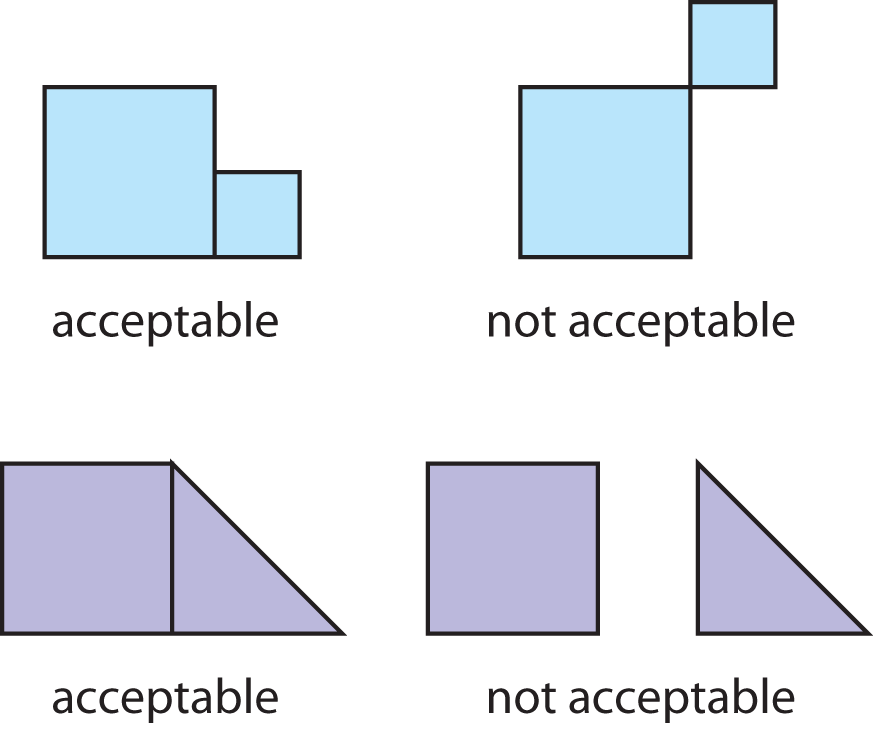
Create Area Riddles. Assign Questions 4–6 for students to complete individually. Students will make their own area riddles. Using a display of the Centimeter Grid Paper Master, establish rules for connecting the pieces as shown in Figure 1. Then allow time for students to draw the shapes for their riddles. Note that the areas for the shapes in Question 4 and 6 are mixed numbers, 812 sq cm and 814 sq cm. Students may use words or symbols to describe the fractional parts.