Use Models to Find Fair Shares. To begin the lesson,
provide access to paper, scissors, and pattern
blocks.
Ask student pairs to solve the following
problem:
- Four girls had 3 pizzas to share fairly. They cut
each pizza into fourths. How many pieces of pizza
did each girl get?
After students have had time to find a solution to the
problem, ask them to share their solution strategies.
Students should find that each girl gets 3 pieces of
pizza. See Figure 2.
- Did each girl get more or less than one whole
pizza? Is that reasonable? (Each girl got less than
one whole pizza. That's reasonable because there
were more girls than pizzas.)
- What model or tools helped you see or represent
the problem? (Possible responses: a drawing;
3 yellow hexagons and 12 brown trapezoids;
3 paper shapes each cut into fourths)
- How did you find out how many pieces of pizza
each girl got? (Possible response: I used 3 yellow
hexagons for 3 pizzas. I put four brown trapezoids
on top of each hexagon to show how to cut
the pizza into four fair shares or fourths. I had
12 brown trapezoids. Then I gave each girl
one trapezoid until all 12 were shared. Each girl
got three trapezoids, so 3 pieces of pizza.) [See
Figure 3.]
Show students three of the identical paper circles
you cut out prior to the lesson. See Materials
Preparation. Tell students to imagine that they are
the girls' pizzas.
- Who can fold each of the circles to show four fair
shares? [Students can fold each circle in half,
and then in half again.]
- Is each of these pizza models divided into 4 equal
parts? Can each model be shared fairly among
four people? How do you know? (Yes; all the
pieces are the same size so it will be fair.)
Cut each pizza model into fourths. Place the pieces
on top of one another to show that they are equal
shares. Remind students that because the wholes are
the same size, each of the fourths must all be equal
in size.
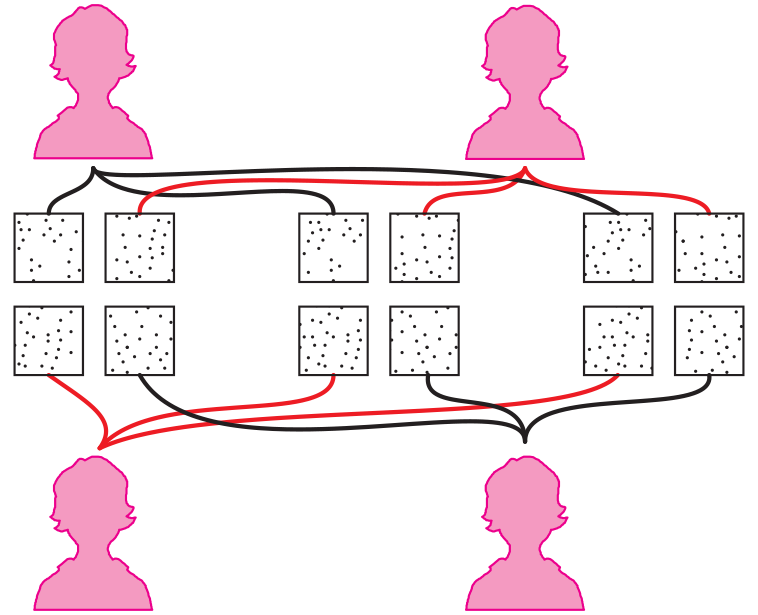
Ask four students to represent the girls in the pizza
problem. Clearly distribute each of the twelve
fourths one by one to each of the four students until
all the pieces have been handed out.
- Did each person get a fair share of the pizza? How
do you know? (Possible response: I can count
each person's number of pieces. Each person has
3 pieces and all the pieces have been shared.)
- How many fourths does each student have? (three-fourths)
- What part of one whole pizza is that? Show us how
you know. (three-fourths of a whole pizza;
Possible response: Each student has three of the
fourths and there are four-fourths in the whole.
Three-fourths is a little less than one whole.)
Take three of the fourths and glue or tape them onto
the different-colored paper circle to model
three-fourths of the whole. See Figure 4.
- How many fourths are in one whole pizza? How do
you know? (four-fourths; Possible response: I can
see that one more fourth piece will fit onto the
pizza model, so one whole pizza would be
one-fourth, two-fourths, three-fourths,
four-fourths.)
Attach the last fourth to the circle.
- Does this model show four-fourths? Count the
fourths. (yes; one-fourth, two-fourths,
three-fourths, four-fourths)
- What is another name for four-fourths? (one
whole)
- How many fourths are in three whole pizzas? How
do you know? (twelve fourths; Possible response:
If each pizza has four-fourths, then
4 fourths + 4 fourths + 4 fourths = 12 fourths.)
Tape the remaining 8 fourths together to make
2 more whole pizza models. Display the three models
containing 12 fourths.
- Let's count all of the fourths on these three whole
pizzas. (one-fourth, two-fourths, three-fourths,
four-fourths, five-fourths, sixth-fourths,
seven-fourths, eight-fourths, nine-fourths,
ten-fourths, eleven-fourths, twelve-fourths)
Finally, show students the last paper circle. Cut it
into four unequal pieces. See Figure 5.
- Did I cut this circle into four parts? (yes)
- Am I showing fair and equal shares? How do you
know? (You didn't cut the circle into fair shares
because not all of the parts are equal in size.
Some are bigger than others so that's not fair.)
- Can I call these parts "fourths"? Why or why not? (No; they are not fourths because a fourth is one
of fourth equal parts. Those parts are not equal.)
Identify Fair Shares. Assign the Fair Shares or Not
Fair Shares pages in the Student Activity Book.
Students will identify the shapes that show fair
shares between 2 (halves), among 3 (thirds), and
among 4 (fourths).
Use Check-In: Question 1H on the Fair Shares or Not Fair
Shares pages in the Student Activity Book to assess
students' abilities to partition shapes into equal shares [E2]
and use words and models to describe equal shares (e.g., half, half of) [E4].
To provide targeted practice, place copies of the Halves and Not Halves, Fourths and Not Fourths, and Thirds and Not Thirds Assessment Masters in a center with scissors and
colored pencils or crayons.
Show Different-Shaped Equal Shares. In the earlier
pizza problem, each fourth was the same shape.
To help students recognize that equal shares of the
same whole do not have to be the same shape, as
shown in Figure 6, distribute one paper square to
each student. See Materials Preparation. Students
will need scissors. Have several extra paper squares
on hand. Tell students to imagine that the paper
square is a sandwich. Explain that everyone has the
same size square. Allow students to compare shapes
with their neighbors if they choose to.
- Luis, Nila, Jackie, and Michael want to cut
one sandwich into fourths so that they can share
it equally. Show how they can do this with your
sandwich model.
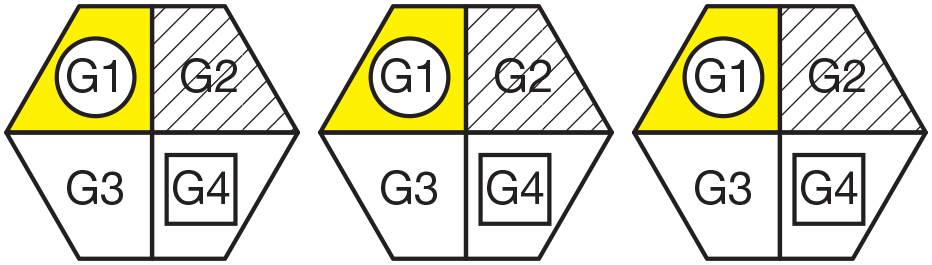
Give students time to fold and cut their square into
four equal shares. Students may divide the square in
different ways. Students will likely show three ways
to make fourths. See Figure 6. Expect some to think
they found other ways by rotating the square. As students
work, circulate about the room and prepare to
select different examples of partitioning the square.
If you would like more examples than the ones you
are seeing, distribute extra squares and challenge an
individual or the class to find other ways to partition
the square.
Select students to display their square sandwich
models. Try to discuss a variety of partitions.
- Let's see how you cut the sandwich into fourths. [See possible responses in Figure 6.]
- Is this example showing four fair shares? How do
you know?
- Can you call each of these parts "fourths"? Why
or why not?
- Let's count each of the fourths. (one-fourth,
two-fourths, three-fourths, four-fourths)
- Are the fourths the same shape? (Possible
response: No, some are shaped like triangles,
some are shaped like squares, and some are
shaped like rectangles.)
- What is the same about all fourths? (Possible
response: They are the same size. They are
one-fourth of the whole.)
- How do you know all of the fourths are the same
size? (Possible response: We all had the same
size square in the beginning and we all cut our
squares into four equal parts, so all the parts have
to be the same size.)
Students should see that there are different ways to
partition the square, but each way must cut the
square into four equal parts. To demonstrate the concept
that equal shares of the same whole do not have
to be the same shape, show students the model you
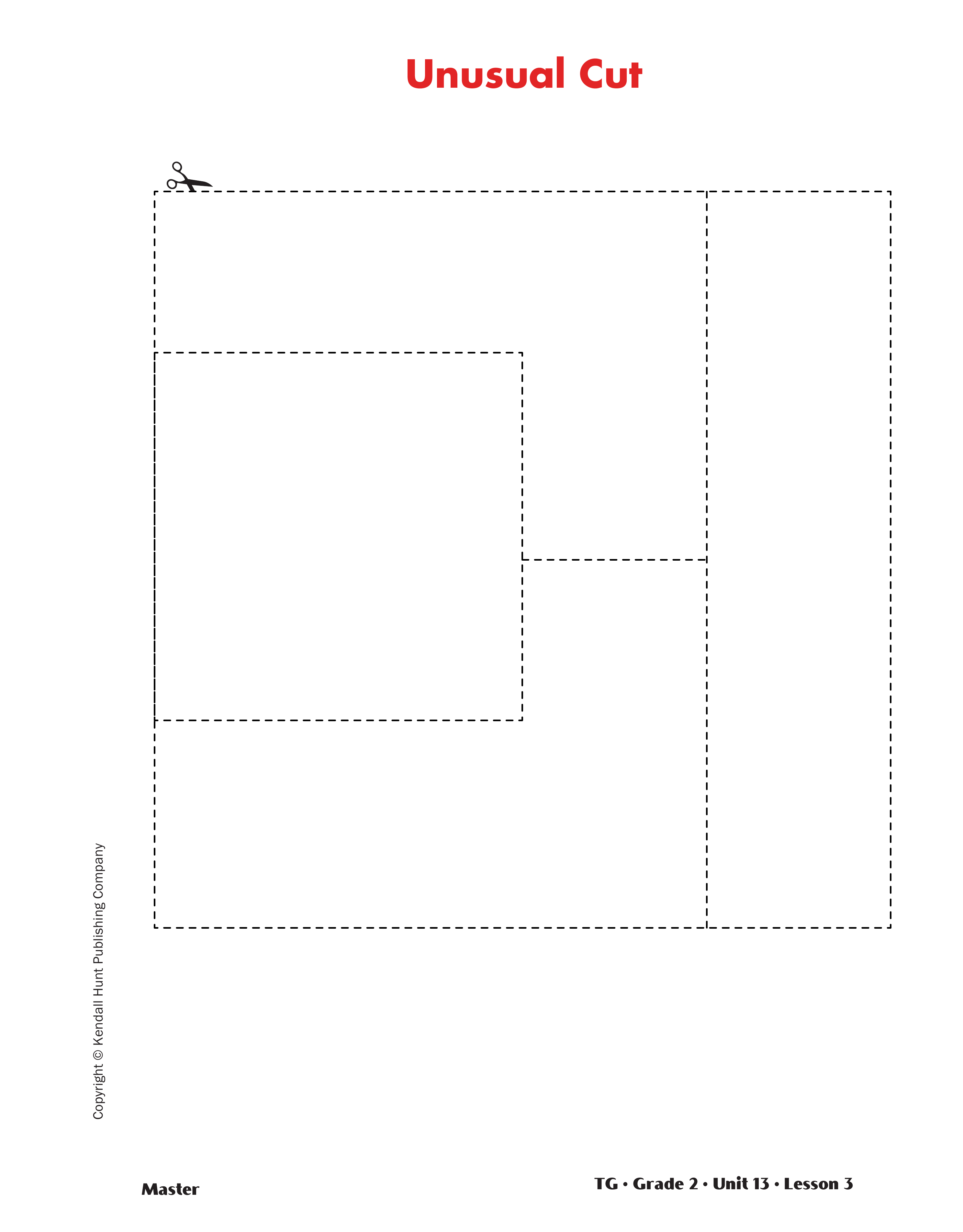
prepared from the Unusual Cut Master. See
Materials Preparation. Use similar questions to discuss
your unusually partitioned square. Tape your
model back together so that students can see that the
four-fourths make a square equal in size to their
square models.
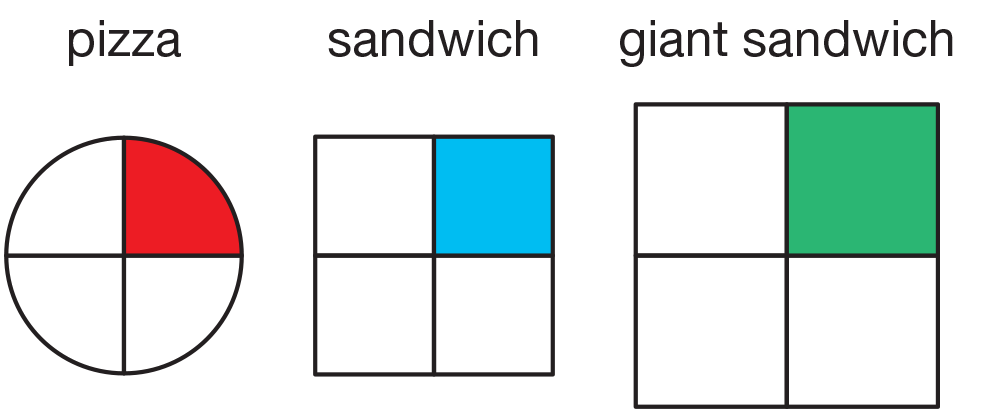
Show Parts of Different-Size Wholes. Review the
concept that the same fractional parts of
different-size unit wholes are not equal. See Figure
7. Ask all the students to examine the "sandwich"
fourths that they made. Display the "pizza" fourths
from earlier in the lesson.
Ask students to compare
the fourths:
- What do you notice? (Possible response: The
pieces are shaped differently.)
- Do both of these models show fourths? How do
you know? (yes; Possible response: We divided
the pizza circle into four equal parts and we
divided the sandwich square into four equal parts
so each part is a fourth of its own whole.)
- Do these fourths look the same? (no)
- Are the wholes the same? (no)
Next ask students to imagine a giant sandwich.
Display the large paper square model you prepared
prior to the lesson. See Materials Preparation.
- Imagine this is a giant sandwich. Could you cut
this into four equal shares or fourths? Show us. (yes)
A student volunteer can fold and cut the large square
into fourths.
- What do you notice about the giant sandwich's
fourths compared to your sandwich fourths? (Possible responses: the giant sandwich fourths
are much bigger than my sandwich fourths; the
giant fourths are the same shape as my fourths;
the giant fourths are shaped differently than my
fourths.)
- Could the giant fourths be the same shape as your
"sandwich" fourths? (Yes, they could be triangles
or squares for instance, just bigger.)
- What is true about all fourths, no matter what the
whole? What is a fourth? (All fourths show four
equal shares of their whole.)
- If the wholes are different from each other, are the
fourths going to be different from each other, too? (yes)