Lesson 4

Partition Rectangles

Est. Class Sessions: 1–2
X

Mathematical Standards

2.G.A
Reason with shapes and their attributes. (2.G.A.2, 2.G.A.3)

Standards for Mathematical Practice

MP1.
Make sense of problems and persevere in solving them.
MP2.
Reason quantitatively.
MP3.
Construct viable arguments and critique the reasoning of others.
MP5.
Use appropriate tools strategically.
MP6.
Attend to precision.
MP7.
Look for and make use of structure.

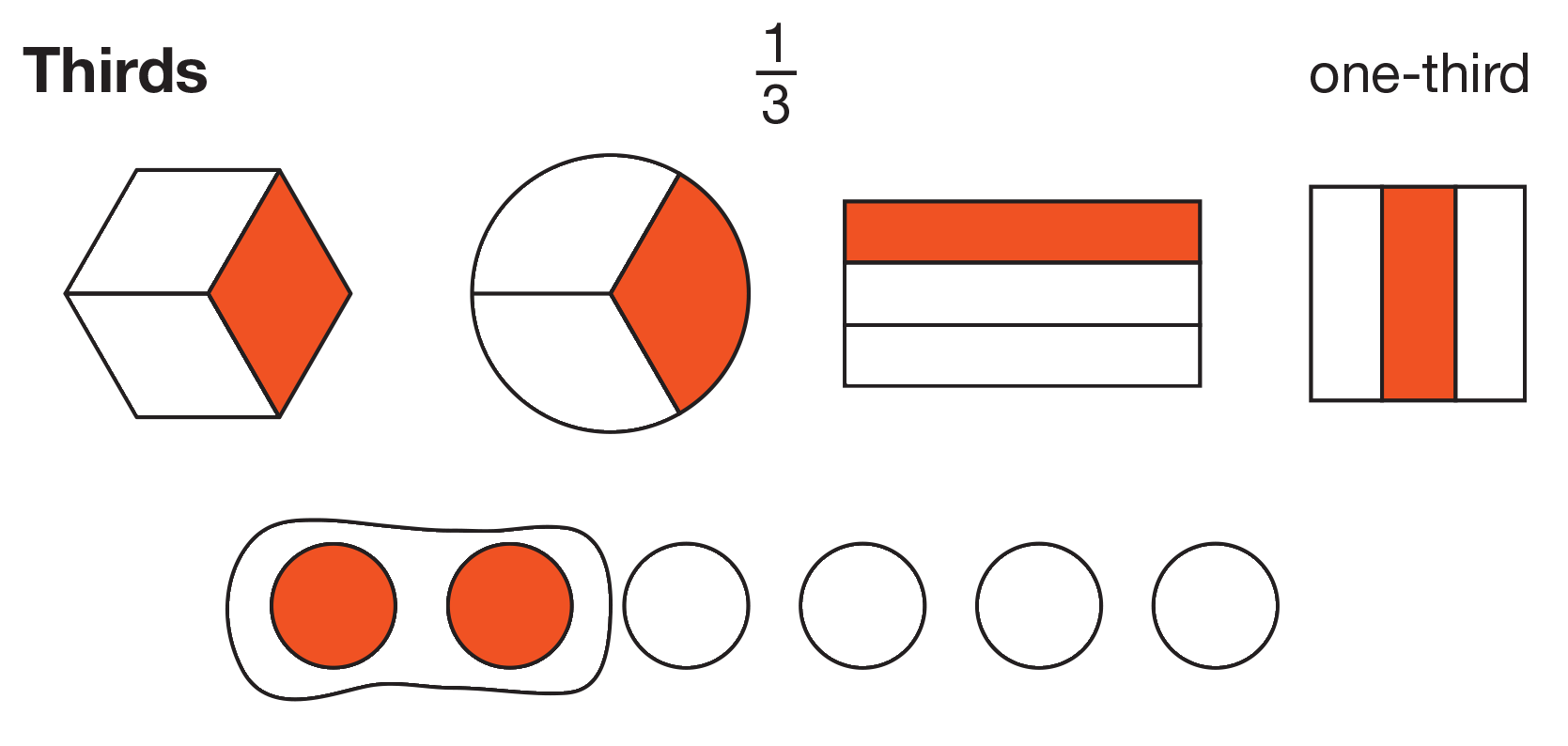
Students use square inch tiles to cover halves, fourths, and thirds of different size rectangles. They partition rectangles into rows and columns of the same size unit and shade one-half, one-fourth, or one-third of the rectangles.

Content in this Lesson

  • Partitioning rectangles into equal shares [E2].
  • Partitioning a rectangle into rows and columns of the same size unit [E3].
  • Using words and models to describe equal shares (e.g., half, half of) [E4].
  • Recognizing that equal shares of the same whole do not have to be the same shape [E5].

Daily Practice and Problems M–N

M. Coin Jar

N. Area Again

X

Materials for Students

Daily Practice and Problems Lesson Homework Assessment

Student Books

 Student Activity Book

Teacher Resources

 Teacher Guide - digital

Supplies for Students

12–15 square-inch tiles
blue crayon or colored pencil
red crayon or colored pencil
centimeter/inch ruler

Materials for the Teacher

Display of 4 Sides and 4 Corners 1 Master (Teacher Guide)
Display of 4 Sides and 4 Corners 2 Master (Teacher Guide)
Display of 2 × 6 Rectangles Master (Teacher Guide).
Unit 13 Assessment Record
Display set of square-inch tiles
centimeter/inch ruler

Assessment in this Lesson

Assessment Expectation Assessed
Partition Rectangles
Check-In: Questions 3–5
with Feedback Box
Student Activity Book
Pages 662–663
E2. 
Partition shapes and sets into equal shares.
E3. 
Partition a rectangle into rows and columns of the same size unit to find the area.
E4. 
Use words and models to describe equal shares (e.g., half, half of).
E5. 
Recognize that equal shares of the same whole do not have to be the same shape.