Reason with Shapes
DEVELOPMENT of FRACTIONS

From a young age, students can share an item with another child or know when something is not shared … read more
From a young age, students can share an item with another child or know when something is not shared fairly. It is recommended that instruction build on students' prior understanding and abilities. Researchers have recommended that students in Second Grade concentrate on developing fraction concepts based on finding fair shares and partitioning shapes into equal shapes. In this unit, students explore sharing and partitioning in two contexts: sharing food or objects and the measurement of area.
This unit begins with problems that students will be able to solve with intuition and by drawing pictures. For example: Jim, John, and Joe are sharing a pie. How much pie will each person get? Students build on those drawings and partition shapes based on pattern blocks. Then students partition rectangular arrays into equal shares and represent those shares with words (halves, fourths, thirds). Finally students apply what they have learned about fractional parts and partitioning rectangular arrays to find the area of shapes with whole and partial units.
Students develop the following fraction concepts and skills:
- Partitioning shapes into halves and fourths;
- Recognizing that the same fractional parts of a whole shape must have equal areas; and
- Representing fractions (halves and fourths) using drawings, numbers, and words.
Students learn that to partition a shape into halves (or fourths) means that the shape is divided into two (or four) parts that have equal areas. They partition shapes by folding them and by counting square centimeters. Figure 1 shows examples of a circle divided into fourths and "not fourths."
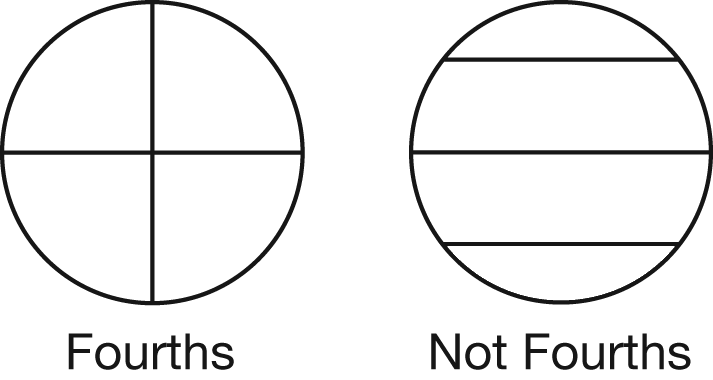
Figure 1: Identifying shapes divided into equal parts
CONCEPT of AREA

Area is the amount of surface covered by a shape, so students discuss the use of standard units to … read more
Area is the amount of surface covered by a shape, so students discuss the use of standard units to cover a shape and then count the units to measure area. Students take part in various activities that develop the following skills and concepts:
- Measuring the area of shapes with straight sides by counting whole and fractional parts of square centimeters;
- Adding fractional parts to find area; and
- Reporting area measurements using a number and square units.
Students begin by finding the area of shapes with whole square centimeters and they progress to more complicated shapes that have fractional parts, either fourths or halves. Over the course of the unit, students develop more efficient methods for counting square centimeters using their knowledge of addition, multiplication, and fractions. For example, students can track their counting of whole and fractional square centimeters by writing numbers in each square as shown in Figure 2.
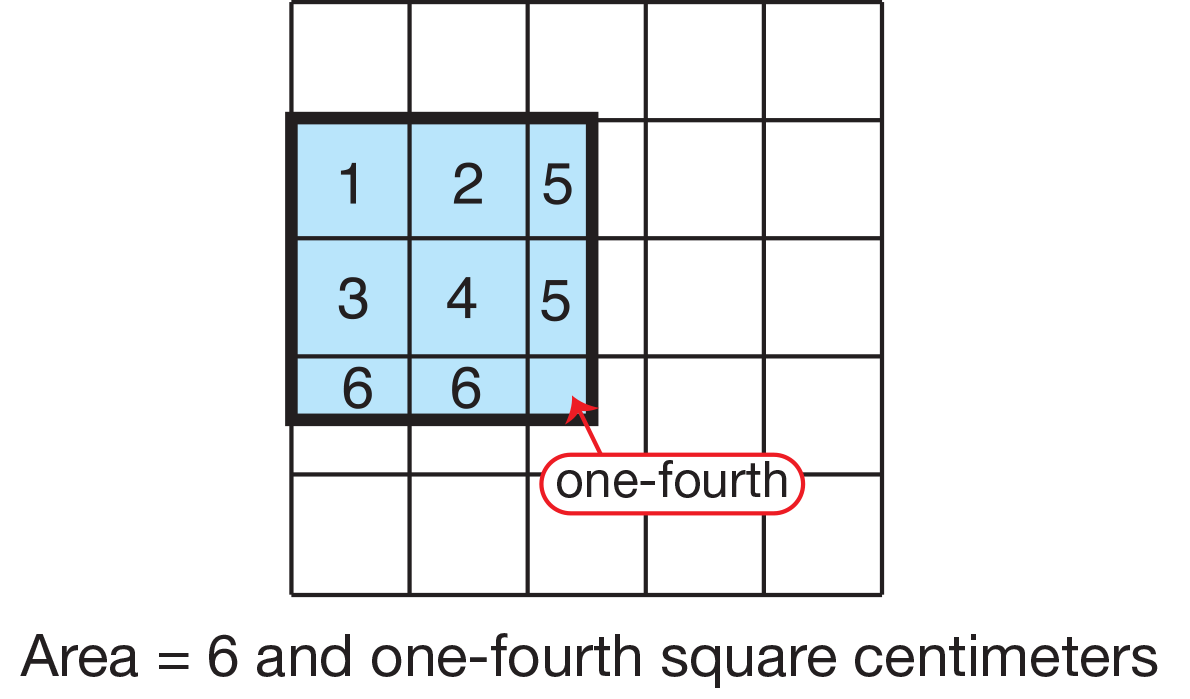
Figure 2: Piecing together fractional square
centimeters when counting areas
With more complicated or larger shapes, students may prefer more efficient strategies as shown in Figure 3.
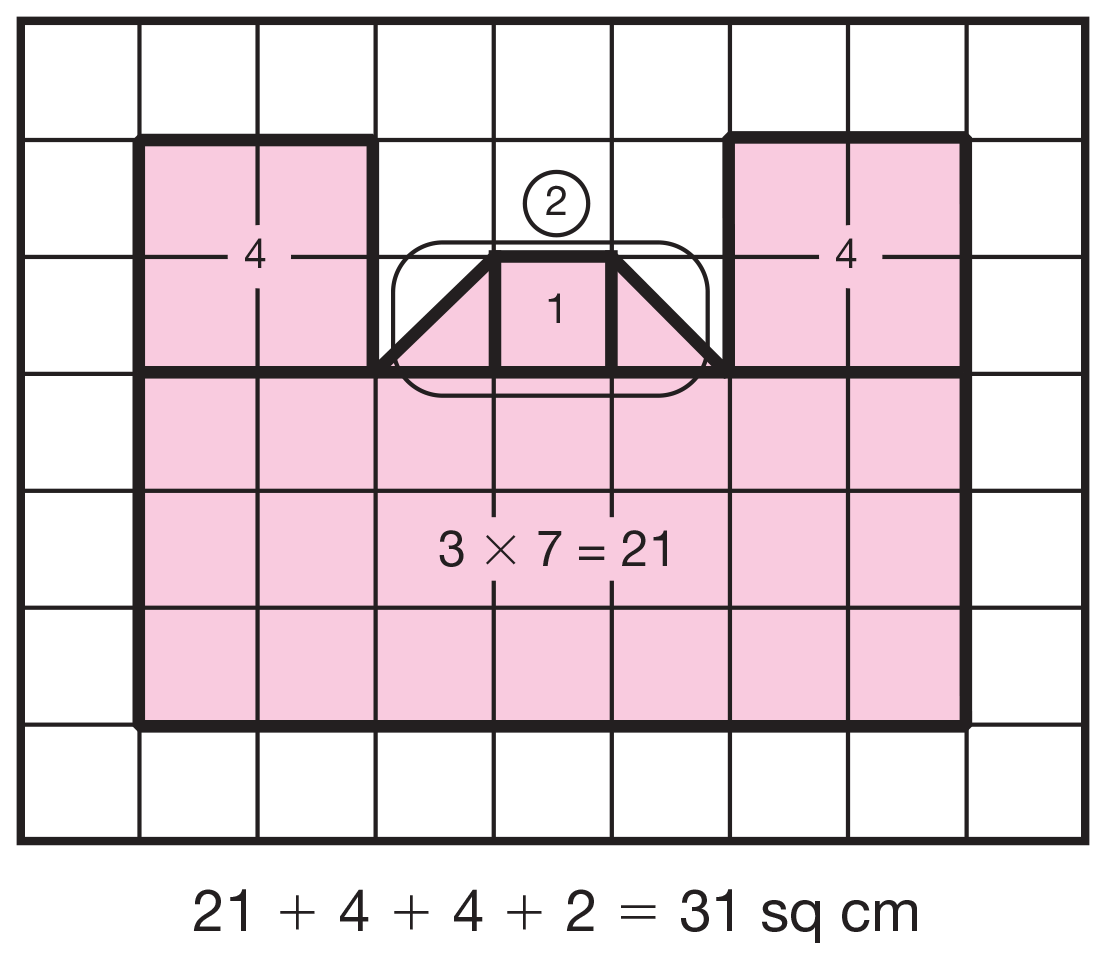
Figure 3: Using multiplication and addition to find
the area of a figure
van HIELE LEVELS of GEOMETRIC DEVELOPMENT

"Given children's affinity toward, knowledge of, and ability to gain geometric knowledge, it is important that … read more
"Given children's affinity toward, knowledge of, and ability to gain geometric knowledge, it is important that this domain of mathematics not be neglected. Instruction in geometry needs to complement the study of number and operation in pre-K to 8" (National Research Council, 2001). Math Trailblazers echoes this expectation by emphasizing the importance of geometry in the mathematics curriculum. This unit represents the focal point of geometry in Second Grade. Students describe, analyze, and classify two-dimensional shapes using their properties. Students also discover relationships within and among these properties as they advance their understanding through stages, from basic intuition to analysis and informal deduction.
Much of the approach to geometry found in the Math Trailblazers curriculum is grounded in the insights of Dutch educators Pierre van Hiele and Dina van Hiele-Geldof. Ongoing research in mathematics education continues to confirm the five levels of geometric development first described by the van Hieles in the 1950s (Burger and Shaughnessy, 1986). The five levels are:
- Level 0: Visualization. Students judge geometric objects by their appearance, but not by attributes. For example, a student can identify a rectangle because it "looks like a rectangle," but not because it has opposite sides equal and four right angles.
Level 1: Analysis. Students begin to describe the properties of objects. A figure is no longer judged because it "looks like one," but rather because it has certain properties. For example, an equilateral triangle has three equal sides, three equal angles, and line symmetry.
Level 2: Informal Deduction. Students logically order the properties of figures and are able to deduce that one property precedes or follows from another property. They see relationships among figures. For example, a square has all the properties of a rectangle; therefore, a square is a rectangle. Students may also be able to define a square based on its properties.
Level 3: Deduction. Students write formal proofs based in an axiomatic system. A rigorous high school geometry course is taught at Level 3.
Level 4: Rigor. Students can work with different axiomatic systems. This level corresponds to college work in geometry (Crowley, 1987; van Hiele, 1999).
The van Hieles found that each level, while not age specific, builds on the previous level. Students proceed from level to level sequentially and no level can be omitted. Advancement depends on content and method of instruction (Crowley, 1987; van Hiele, 1999). Moreover, a student's experiences with lower-level reasoning at the elementary school level are critical to success with geometry in later schooling. Students who are at Level 0 or 1 when entering high school geometry have a poor chance of success. Students who begin high school geometry at Level 2 have at least a 50% chance at succeeding (Senk, 1989). Unfortunately, many upper elementary students are still at Level 0. This is not surprising, as researchers have found that most geometry questions asked in standard elementary math textbooks were answerable with Level 0 understanding (Fuys, Geddes, and Tischler, 1988).
In this unit, we start with Level 0 ideas by asking students to identify and draw various geometric figures. Most of the work in this unit is at Level 1, where students describe the properties of two-demensional shapes. Level 2 ideas are introduced as students explore ways to classify these figures.
A WORD on VOCABULARY

This unit contains a great deal of mathematical vocabulary. Encourage students to use mathematical words … read more
This unit contains a great deal of mathematical vocabulary. Encourage students to use mathematical words that precisely and accurately express their thoughts. However, keep in mind that students remember definitions with greater meaning when they learn them through discourse. Direct memorization is generally far less productive than using words in context, since words learned by rote are quickly forgotten. A better strategy is to encourage students to discuss their work using their language and then model geometers' terminology to extend the discussion.
Etymology, or the study of words, teaches us that words often do not have an exact, single meaning. Word meanings evolve over time, and words may be defined differently among different groups or individuals. This is even true in mathematics. For example, in a study of school geometry texts, the word "quadrilateral" was found to have seven different definitions (Usiskin, 2008). Although each of these definitions includes the same set of shapes, each emphasizes something different about quadrilaterals. When considering the word "trapezoid," we even find two definitions in textbooks that include different sets of shapes. One definition includes quadrilaterals with only one pair of parallel sides; another with at least one pair of parallel sides. In the end, the class must agree to settle on a particular definition, but we should do so knowing mathematicians sometime disagree.
MATH FACTS and MENTAL MATH

Subtraction Facts
Daily Practice and Problems items in this unit can be used to assess students' fluency with the … read more
Subtraction Facts
Daily Practice and Problems items in this unit can be used to assess students' fluency with the subtraction facts related to the addition facts in Group E (11 − 1, 11 − 10, 12 − 2, 12 − 3, 12 − 4, 12 − 5, 12 − 7, 12 − 8, 12 − 9, 12 − 10, 13 − 3, 13 − 4, 13 − 5, 13 − 8, 13 − 9, 13 − 10, 14 − 5, 14 − 9). Counting-on, counting-up, and counting-back strategies are most commonly used to solve these facts.
Resources
- Burger,W., and J.M. Shaughnessy. "Characterizing the van Hiele Levels of Development in Geometry." Journal for Research in Mathematics Education, 17 (1), pp. 31–48, 1986.
- Clements, D., and J. Sarama, Learning and Teaching Early Math: The Learning Trajectories Approach. Routledge, New York, 2009.
- Crowley, M.L. "The van Hiele Model of the Development of Geometric Thought." In Learning and Teaching Geometry, K–12. 1987 Yearbook. Mary Montgomery Lindquist ed. National Council of Teachers of Mathematics, Reston, VA, 1987.
- Fuys, D., D. Geddes, and R. Tischler. "The van Hiele Model of Thinking in Geometry Among Adolescents." Journal for Research in Mathematics Education, Monograph Number 3. 1988.
- National Research Council. "Developing Mathematical Proficiency beyond Number." In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- Senk, S.L. "Van Hiele Levels and Achievement in Writing Geometry Proofs." Journal for Research in Mathematics Education, 20 (3), pp. 309–321, 1989.
- Usiskin, Zalman. The Classification of Quadrilaterals: A Study in Definition. Information Age Publishing, Charlotte, NC, 2008.
- van Hiele, Pierre M. "Developing Geometric Thinking through Activities That Begin with Play." Teaching Children Mathematics, 6, pp. 310–316. 1999.
- Wilson, Patricia R., and A. Osborne. "Foundational Ideas in Teaching about Measure." Teaching Mathematics in Grades K–8, Research-Based Methods. Thomas R. Post ed. Allyn and Bacon, Inc., Boston, 1988.












