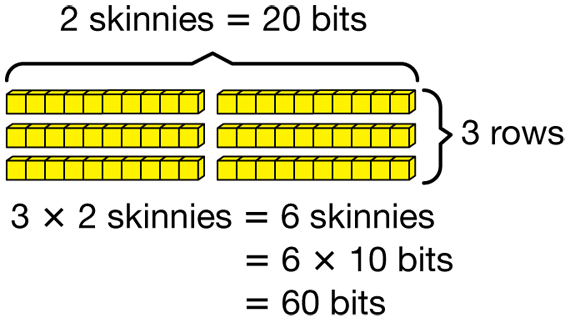Multiply by Ten. Begin by briefly reviewing the term multiple of ten in the name of the lesson.
- What is a multiple of ten? (A multiple of ten is any number that you get when you multiply by ten.)
- Find 10 × 2, 10 × 5, 10 × 10, 10 × 12, and 10 × 10 × 5. (20, 50, 100, 120, 500)
- What pattern do you see in multiples of 10? (They all end in zero.)
- How much is 2 tens? 5 tens? 10 tens? 12 tens? 50 tens? (20, 50, 100, 120, 500)
Together read the opening vignette, Reach for the Stars, on the Multiplying by Multiples of Ten pages in the Student Guide. Discuss various ways to think about 3 × 20 using Question 1. Students may remember that to multiply 3 × 20, they need only multiply 3 × 2 and append an extra zero. Other students may explain this as taking 3 groups of 20, tripling 20 to get 60, or multiplying 3 times 2 tens.
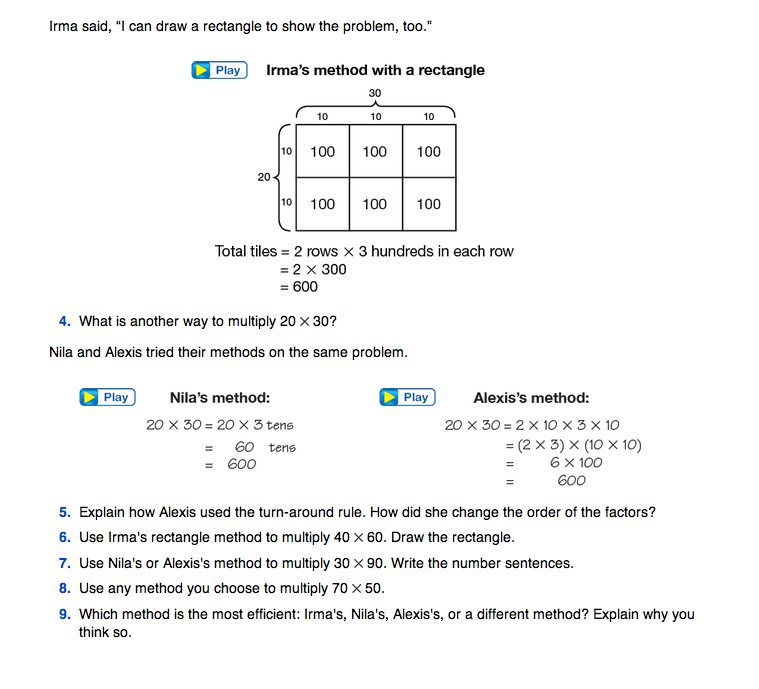
Discuss Irma's use of base-ten pieces for solving the problem. See Figure 1.
Base-ten pieces are shown in this lesson as a model for multiplication by multiples of 10. Students need not use base-ten pieces in this lesson if they can readily make sense of the diagrams in the Student Guide pages. However, for students who have difficulty understanding the place value concepts involved in multiplication, it may be helpful for them to model and solve some of the problems in this lesson with base-ten pieces.
Have a display set of base-ten pieces available, and ask:
- Can you explain how Irma solved the problem with base-ten pieces? (She showed three rows of 20 stars by making three rows with two skinnies in each row. Then she counted up all the skinnies and multiplied by ten, since there are ten bits in one skinny.)
- How does Irma's method compare to your method? Did both methods give the same answer?
Read and discuss Nila's and Alexis's methods for solving the same problem.
- How are these methods alike? (They both break apart the 20 before multiplying.)
- How are they different from each other? (One uses the word “tens” and the other uses the number “10” as a multiplier.)
- How are they like Irma's method? (Irma's method breaks each group of 20 into 2 tens, just like these methods do.)
So that students become comfortable with the terms factor, product, and multiple of ten, model using them in the discussion and encourage students to use them in their explanations when appropriate.
Have students work in pairs to solve the problems in Question 2 using Nila's or Alexis's method. Emphasize the place value meaning in these problems. That is, 2 × 70 is not simply 2 × 7 with an extra zero; rather, it is 2 × 7 tens, or 2 × 7 × 10.
Use the Commutative Property. Use the next part of the vignette and Question 3 to discuss using the commutative property to solve problems where the multiple of ten is the first factor in a problem, such as with 20 × 3. Using the commutative property or turn-around rule will rearrange the factors into a more convenient order without changing the product. See Content Note.
Students may already be able to consistently apply a rule for appending place-holding zeros to the end of a product. However, it is important that students understand the place value concepts behind this method. Several models will be introduced that connect the rule to its underlying concepts. This will help struggling students remember the concept and challenge others to use algebraic properties to justify their answers. Throughout the lesson, ask students to show and explain various methods for multiplying by multiples of ten that demonstrate understanding of the concepts leading to the rule.

Commutative Property of Multiplication. This property says that the order of factors in a multiplication sentence does not matter. Students may use the term turn-around rule instead of commutative property.
For students to appreciate the commutative property of multiplication, ask them to consider whether other operations are commutative. Addition is commutative (40 + 20 = 60 and 20 + 40 = 60). Division is not commutative: 60 cookies divided among 30 children gives two cookies per child (60 ÷ 30 = 2 cookies). However, 30 cookies divided among 60 children gives only one-half cookie per child (30 ÷ 60 = 1/2 cookie).
The commutative property has to do with the order in which things can happen. Putting on your shirt and jeans is commutative (the order in which you do it does not matter). However, putting on your shoes and socks is not commutative (the order certainly does matter).
The commutative property is very useful when multiplying by multiples of ten. However, research shows that some students do not automatically use the commutative property when solving a problem such as 20 x 3. Rather than thinking about 20 x 3 as 3 sets of 20 (as they would with 3 x 20), they may think about it as 20 sets of 3. This ordering can lead to solving the problem with an inefficient strategy, such as skip counting by threes 20 times. Discussing the turn-around rule may help these students reorder the factors to solve the problem more easily.
Multiply Larger Factors. Read through the next part of the vignette involving the multiplication problem 20 × 30. Continue discussing Questions 4–9. Allow students to work on problems in pairs or groups.
Nila's method helps students see the place value meaning of the zeros that are appended when multiplying multiples of 10. Alexis's method shows this mathematically. Use Question 5 to help students describe the use of the turn-around rule.
3 × 10 × 2 × 10
is recorded as
(3 × 2) × (10 × 10)
Students are asked to consider the efficiency of different methods in Question 9.
- What makes Nila's method efficient? (It breaks the problem into smaller, simpler calculations.)
- Is Irma's rectangle method efficient? (It is not as quick as Nila's or Alexis's method, but it can help make sense of the problem.)
- Is using a calculator always efficient?
Using a calculator is efficient when the numbers are not “friendly” or convenient. However, if buttons are pushed incorrectly, wrong answers may result. We still need good ways to estimate products to check for reasonableness. However, when the numbers are convenient, such as multiples of ten, using a calculator may be less efficient than using mental math.
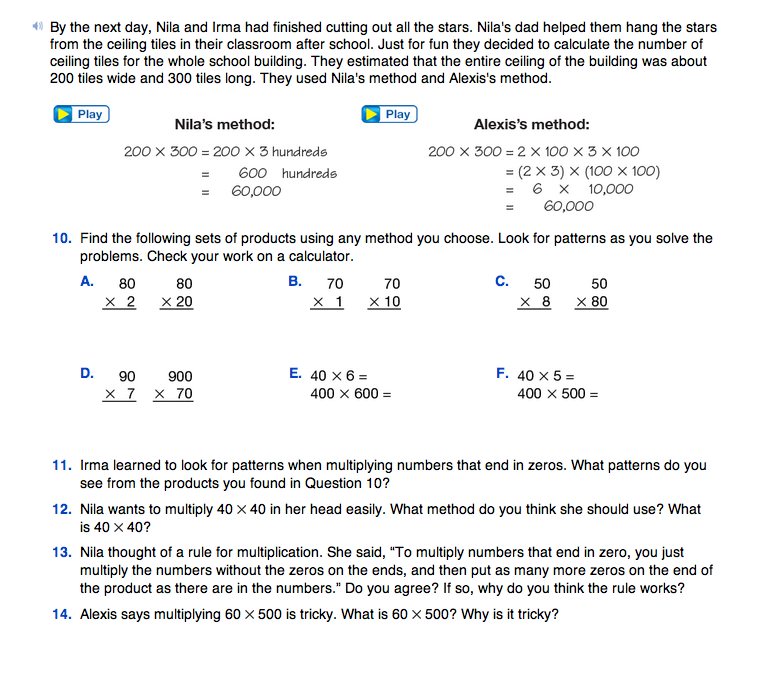
In Questions 10–17, students find products of larger numbers (up to three digits) ending in zeros.
When discussing Nila's pattern in Question 13, make sure students recognize that the pattern does not apply to zeros in the middle of a number, such as the zero in 6024. Similarly, help students to recognize that, sometimes, an extra zero is formed from multiplying the nonzero digits. For example, in Question 14, 60 × 500 is 30,000. There are 4 zeros because an extra zero was formed from 6 × 5 = 30.
Do more problems together as a class to help students practice mental math strategies:
70 × 10
70 × 100
70 × 1000
700 × 10 |
70 × 20
70 × 200
70 × 2000
700 × 20 |
40 × 50
40 × 500
40 × 5000
400 × 50 |
Practice Multiplying by Multiples of Ten. The Practice Multiplying with Tens pages in the Student Activity Book provide a menu of differentiated practice. You may use this as in-class work or as homework.