Divisibility Rules

Est. Class Sessions: 2

Developing the Lesson

Part 1. Divisibility by 2 and 3

Create a bulletin board or use chart paper to display the divisibility rules. As students explore multiples of 2, 3, 5, 6, 9, and 10, add rules for identifying each. Students may use the display as a reference.

Divisible by 2. Read the opening vignette on the Divisibility Rules pages in the Student Guide. Shannon, Roberto, and Ming are discussing whether 318 is divisible by 2. Ming reasons that 318 is divisible by 2 since 318 ÷ 2 has no remainder.

Questions 1–4 in the Student Guide discuss numbers that are divisible by 2.

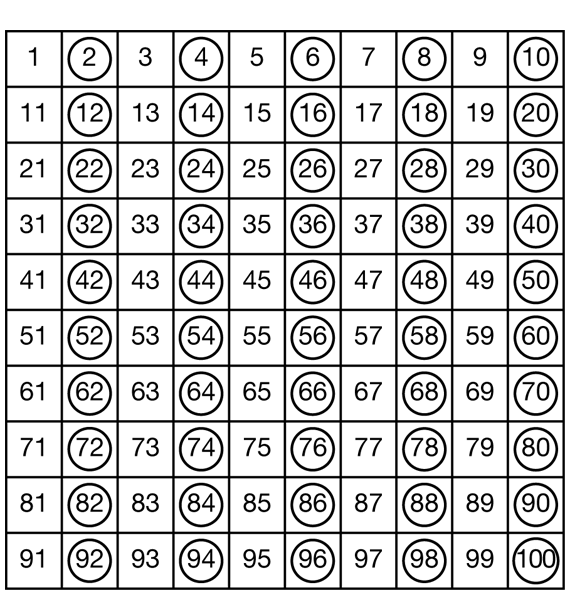
It is worthwhile for students to see the pattern that emerges when the multiples of two are circled on the 100 Chart as shown in Figure 1. Using a display of the 100 Chart Master, circle the multiples of 2 in blue along with your students. Students should see that all multiples of 2, or even numbers, end in 0, 2, 4, 6, or 8. The even numbers form five straight columns on the chart.

Question 2 asks students to extend the pattern they see to larger numbers.

The number 318 would fall in the same column as the 8, 18, 28, 38, etc., since the ones digit is 8. No matter how large a number is, the digit in the ones place tells us whether the number is even or odd.

Some students may recognize which numbers in Question 3 are evenly divisible by 2 without a calculator. However, in order to write multiplication and division number sentences, calculators should be made available (Question 3B). If a number is divisible by 2, the answer in the calculator window will be a whole number. When a number is not divisible by 2, a whole number does not result.

Divisible by 3. Have students turn to the Is It Divisible by 3? section in the Student Guide. Three pairs of related multiplication and division sentences are listed to show that the numbers 12, 21, and 30 are divisible by 3. Emphasize that a number is divisible by 3 if 3 is one of its factors.

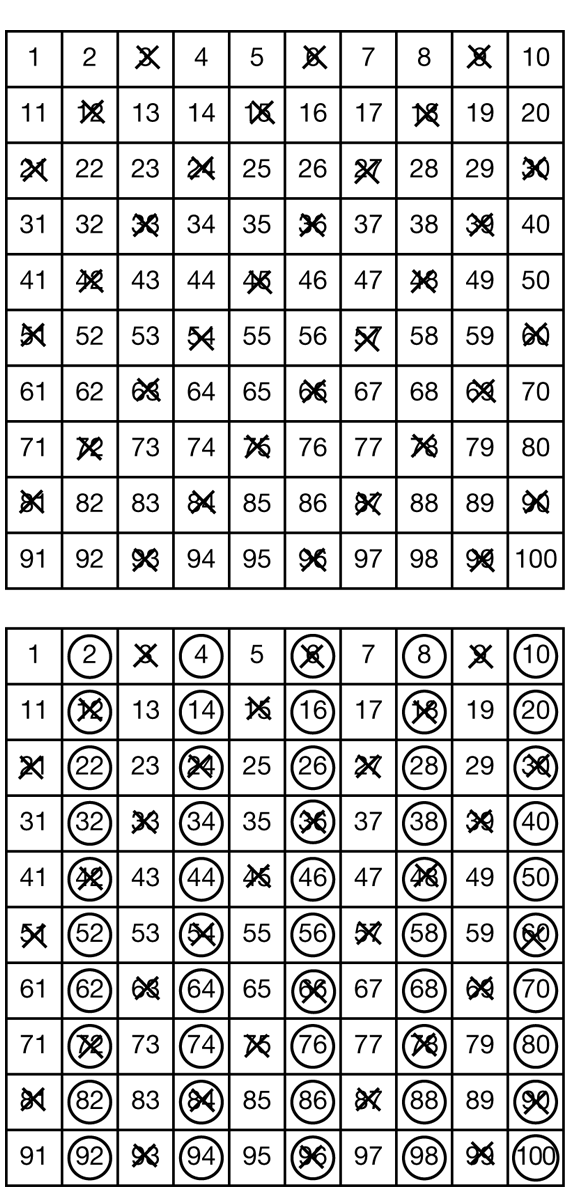
Avoiding confusion. When a number divides into another without remainder, we say it divides evenly. For example, 3 divides evenly into 27 since 27 ÷ 3 = 9. The meaning of the word “evenly” in this situation comes from the sharing model of division—something is divided evenly into groups if all groups get the same amount with nothing left over. Be aware that some students might be confused with this use of the word “even” because they might assume “even” has something to do with even numbers. They might think that 3 divides 24 evenly because the answer to 24 ÷ 3 is an even number (8) and incorrectly think 3 does not divide 27 evenly because 27 ÷ 3 is an odd number (9).

Use Questions 5–11 to guide a discussion about divisibility by 3. Students mark a red “X” on all of the multiples of 3. As they are marking the numbers, stop them periodically and ask them to say a multiplication or division sentence for a specific multiple of 3.

For example, as a child skip counts by three and marks 18 with a red “X,” ask:

Tell me a multiplication sentence that shows 3 is a factor of 18. Tell me a division sentence that shows that 18 is divisible by 3. (3 × 6 = 18; 18 ÷ 3 = 6)

Ask students to look for patterns in those numbers marked in red—the multiples of 3. The multiples of three form six diagonals through the 100 Chart as shown in Figure 2. Some students may say the multiples of 3 are not as easy to identify as the multiples of 2. A multiple of 3 can end in any number. Multiples of 2 end only in 0, 2, 4, 6, or 8 (Question 6).

In Questions 7–10, students use their copies of the 100 Chart and calculators to determine if a number is divisible by 3. These problems also provide further practice in writing related multiplication and division sentences.

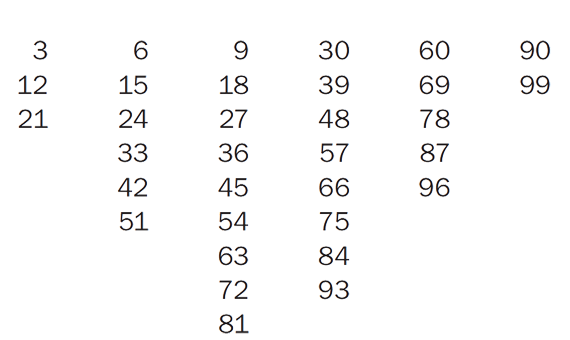
Help students focus on the multiples of three by writing the numbers in each diagonal on the chalkboard as shown in Figure 3. When looking at the multiples of 3 this way, students may recognize some of the following patterns:

The multiples of 9 appear in the third column.
The numbers in each column increase by 9 as you read the numbers from top to bottom.
The digits in the tens place increase by one as you go down the first three columns. The digits in the ones place decrease by one as you go down each of the first three columns. The remaining columns also decrease by one in the ones place, but they start with a zero.

Students who notice the multiples of 9 listed may begin to ask such questions as, “Does this mean numbers that can be divided by 9 evenly can also be divided by 3 evenly?” You may wish to pursue this now or tell students that later they will investigate the multiples of 9. Students may reason that a multiple of 9 or a number divisible by 9 is also divisible by 3 since 3 is a factor of 9.

One or two students may recognize that the sum of the digits of a multiple of three is also a multiple of 3. Students may question whether this pattern continues.

We suggest that you do not proceed to Question 11 until students have investigated patterns and shared their thoughts. When you feel it is appropriate, ask student pairs or groups to read and discuss Mrs. Dewey's data table in Question 11.

Some students may note that some of the numbers they marked red were already circled in blue. These students are on their way to exploring divisibility by 6. The numbers that are marked in red and circled in blue are multiples of 6.

Later in this lesson, students will explore divisibility of 6 by looking at the multiples of 6, the multiples of 2, and the multiples of 3. Students should keep this copy of the 100 Chart in a safe place since the same copy will be used throughout the lesson.

After students have had some time to discuss it, display the table from Question 11. If a pair of students recognizes the pattern (a number is divisible by 3 if the sum of its digits is a multiple of 3), ask them to explain it. If not, list additional multiples of three and the sum of their digits, extending Mrs. Dewey's data table.

Ask:

What is the “sum of the digits” for each number in the table? Write an addition sentence. (For 18, 1 + 8 = 9, for 42, 4 + 2 = 6, etc.)

Point out that the sums are multiples of three (e.g., 198 is a multiple of 3: 1 + 9 + 8 = 18. 18 is a multiple of 3).

Then, ask students to name some numbers from their 100 Charts that are not divisible by three and test those numbers (e.g., 88 is not a multiple of 3: 8 + 8 = 16. 16 is not a multiple of 3). The sums of the digits of these numbers are not multiples of 3.

List numbers on the board:

103 111 192 1236

Have students use the divisibility rule for 3 to predict whether or not each number is divisible by 3. Have them check each one on a calculator using division. The numbers 111, 192, and 1236 are divisible by 3.

When students are ready to proceed independently, assign Questions 12–15 for practice or for homework.