Order of Operations

Est. Class Sessions: 2

Developing the Lesson

Part 1. Order of Operations

Introduce Operations. Use the Order of Operations pages in the Student Guide to explain the order of operations.

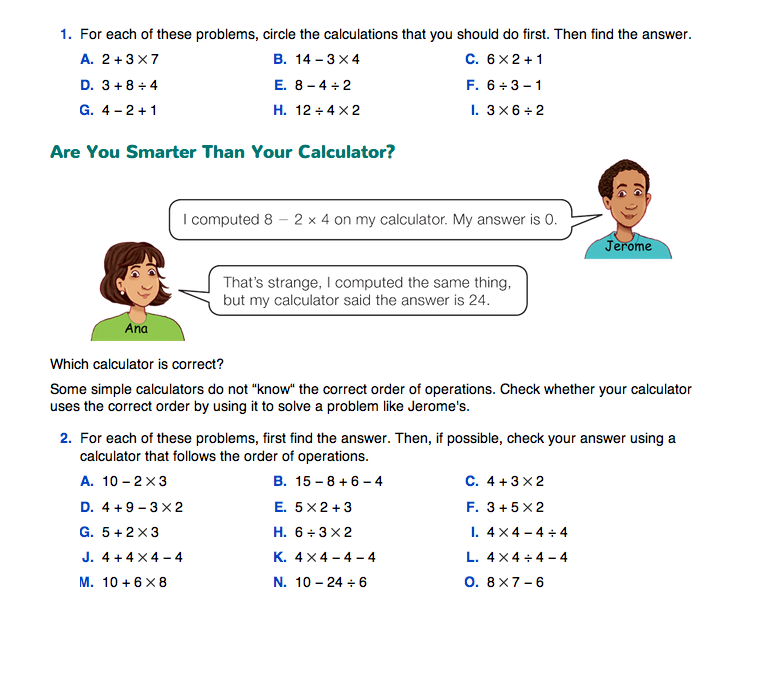
These pages first introduce the meaning of the word “operation.” They show a problem, 3 + 2 × 6 = 15, that illustrates the need to agree on an order in which operations are performed. After reading about the order of operations rule, ask students to solve the problems in Question 1. In these problems, students should circle the calculations they will do first, then do the calculations. Note that in Question 1G, subtraction is done first. Since subtraction and addition have the same level in the order of operations, they are done from left to right. Similarly, division is done first in Question 1H and multiplication is done first in Question 1I. Since multiplication and division are at the same level in the order of operations, they are done from left to right.

Some teachers have reported difficulty finding a calculator that does not follow the order of operations. If such a calculator is not available to you, explain to students that such calculators used to be commonly used in grade schools, but now they are not as easily found. For the Checking Calculators activity on this page, ask for a student volunteer to pretend to be the “old-fashioned calculator” which does not follow the order of operations. Instruct the student to solve the problems in the activity by performing all operations from left to right. Then compare the student's answers with those given by the calculator that uses the order of operations.

Adapt the discussion prompts as necessary to make the same points about checking calculator answers, understanding why answers may be different when not following the order of operations, and adapting one's use of noncompliant calculators.

Check Calculators. In the Are You Smarter Than Your Calculator? section in the Student Guide, Jerome and Ana get different answers using two different calculators. Students should check that the correct answer is 8 − 2 × 4 = 0, so Jerome's calculator is correct. Ana's calculator does not follow the correct order of operations. Ask students to check whether their own calculators follow the correct order. Do they get Jerome's answer or Ana's answer to 8 − 2 × 4?

Next, compare calculators that follow the order of operations with those that do not. If using actual calculators, hold up two calculators, one that uses the conventional order of operations and one that does not. Do not tell students which is which; they will figure this out. Write a problem on the board such as 6 − 3 × 2. Pass out the two calculators to two different students and have them solve this problem on the calculators by entering the following keystrokes:

Write the solutions the calculators give on the board. Calculators that follow the order of operations will give a solution of 0. Calculators that do not follow the order of operations will give a solution of 6.

Ask:

Which calculator is correct? How do you know? (The calculator that answered 0 is correct. I checked by computing the answer myself. I did the multiplication first.)
Can you figure out how the other calculator must have done the calculation? (I think it did the subtraction first. If it found 6 − 3 = 3 and then multiplied by 2, it would get 6.)
Why do different calculators give different answers to the same problem? (They don't all follow the same order of operations.)
What order did the calculator that did not get the correct answer probably follow? (It probably did the calculations in the order they were entered—everything from left to right. The calculator probably isn't fancy enough to remember everything at once, so it just computed as it went along.)
How can you check whether you have a calculator that doesn't use the correct order of operations? (Try a problem where you aren't supposed to do the calculations from left to right. In Jerome's problem 8 − 2 × 4 you should do the multiplication first. But a simple calculator would subtract first since subtraction comes first when you go left to right.)

Explain that calculators that do not use the correct order of operations can still be useful—they just can't be trusted to do a string of calculations. Ask students to think about how to compute something like 3 − 12 × 4 on a calculator that does not use the conventional order of operations.

Ask:

Which calculation should be done first when finding 3 − 12 × 4? (The multiplication, because multiplication always comes before addition.)
What is the answer on a calculator that uses the correct order? (51)
How can you solve the problem if your calculator doesn't use the correct order of operations? (You can have the calculator do the computations one at a time. First type in 12 × 4 = _____. It will tell you 48. Then add 3. It will give 51.)
So the calculator still does the calculations, you just have to tell it the order.

Question 2 provides more practice with the order of operations and with calculations on calculators that use the correct order of operations. Assign the problems and be sure students predict what a calculator will show before they solve each problem.

Assign Home Practice Part 2 as in-class work or homework. Discuss student answers. In particular, ask about Question 1H. The single division operation in between two addition and subtraction operations seems to be confusing to some. Applying the order of operations correctly, the answer is 103.

100 − 49 ÷ 7 + 10 = 100 − 7 + 10 = 103

If students are having trouble deciding which operations to do first, encourage them to circle multiplications and divisions and do them first, from left to right. Then do the additions and subtractions from left to right.

Use Parentheses. The Parentheses section in the Student Guide shows how parentheses can be used to clarify the order in which to do calculations. The calculations inside the parentheses are done first. In the first example in the Student Guide, (6 − 2) × 3, the parentheses say that the subtraction should be done first. This overrides the rule that multiplication is done first. In the second example, 6 − (2 × 3), the parentheses say that the multiplication should be done first. This agrees with the rule, so the parenthe- ses are not actually needed. They are sometimes included as a reminder, however. Suggest to students that the parentheses play a role similar to the circles they used earlier in the lesson, by showing how to group the calculations.

In Question 3 students solve problems that involve parentheses. Question 4 asks students to explain how they could find out whether a calculator uses the correct order of operations.