Multiplication Strategies for Larger Numbers

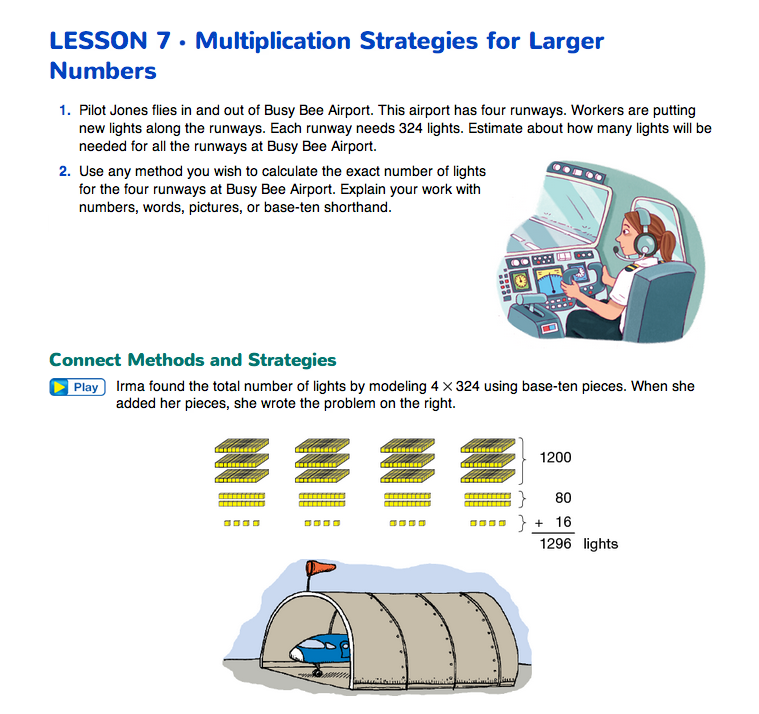
Connect Multiplication Strategies. Have students solve the problems in Questions 1 and 2 on the Multiplication Strategies for Larger Numbers pages in the Student Guide. Give them a few minutes to estimate and then find exact answers. Ask a few students to share their estimation strategies and their methods for solving the problems.

As students work through Questions 3–20, alternate class discussion with small group or partner work. Questions 3–9 ask students to identify and explain similarities and differences between the different paper-and-pencil methods: all-partials, rectangles, and using expanded form. This is an important part of the conceptual basis for a deep understanding of the multiplication process. Try to involve as many students as possible in the discussion.

Copy the student solutions given in the book on the board or display the Three Paper-and-Pencil Methods Master. Have your students come to the display or board to point to the steps or parts of the solutions as they explain the similarities and differences. Ask additional questions that require students to identify and refer to place value when giving their explanations.

Question 10 involves multiplication of a number that has a zero in the tens place.

Pose a few similar problems for students to solve, such as:

609 × 5          360 × 4

Encourage them to use both mental math and paper-and-pencil methods.

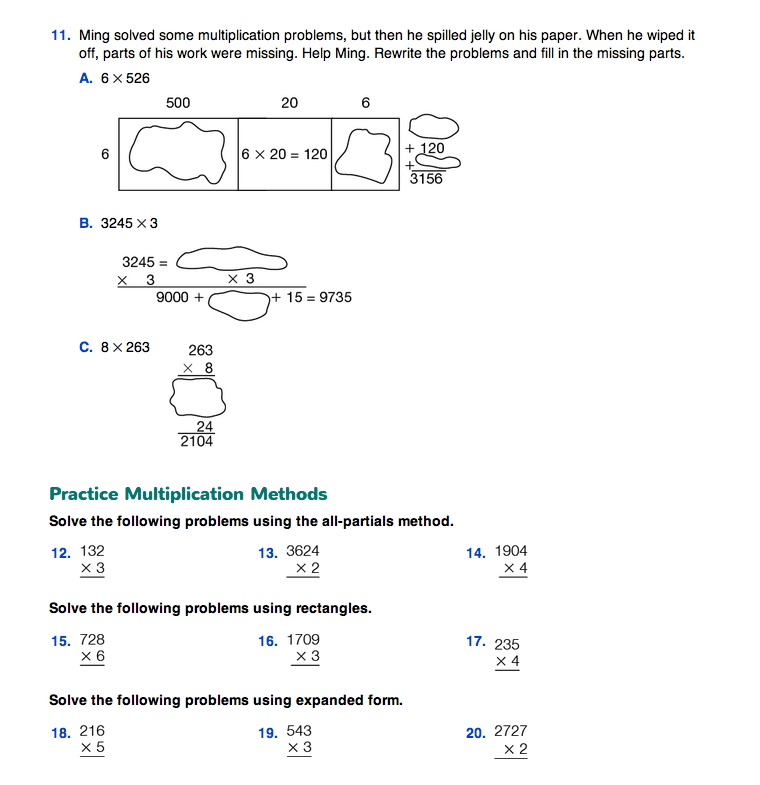
Question 11 provides additional scaffolding. Students look at work partially completed by another student and analyze what was done or what is missing.

Practice Multiplication Methods. Have students answer Questions 12–20 individually or with a partner. Ask volunteers to demonstrate solving the problems using the method requested.

Compact Method. In the vignette before Question 21, Keenya explains how she solved the airport lights problem in Question 2 using the compact method. Have one student read the explanation aloud while another student shows the solution step-by-step on a display or board. The explanation given in the Student Guide makes frequent mention of place value to draw attention to the underlying rationale for the steps of the compact method. Questions 21–22 ask for comparisons with other paper-and-pencil methods.

Display and discuss Question 23. Use this question to deepen students' connections between the compact method and place value concepts. Questions 23A–E ask students to identify and explain each step in solving a problem using the compact method. Be sure students use place value in their explanations. For example, ask students to tell what the little numbers they write down represent. That is, the little 2 above the tens column in Question 23 is 20, or 2 tens, not 2.

Questions 24–28 provide practice using the compact method and estimating to check reasonableness. In Question 29, students find a mistake in a solution and solve the problem correctly.

Questions 24 and 29 model using estimation to determine whether one's answer is reasonable or not.

Ask student pairs to discuss Question 30. Students are asked to write a letter comparing the compact method to the expanded form strategy for multiplication. Students should talk with their partners about the similarities and differences in the two strategies and then each student should write his or her own letter.

At this point, assign Questions 1–5 of the Homework section in the Student Guide.