The unit begins with an exploration of the order of operations. This is the order that mathematicians have agreed upon when completing calculations in an expression such as 8 − 3 × 2. However, this order is not arbitrary. It assigns priorities to operations and specifies when to complete operations of the same priority. Basically, more sophisticated operations have priority over less sophisticated operations. Operations with the same priority are done from left to right. Multiplication and division have the same priority and, since they are more sophisticated than addition and subtraction, they are done first. Thus, 8 − 3 × 2 = 8 − 6 = 2. Since addition and subtraction have the same level of sophistication, they have the same priority. Thus the operations in 8 − 3 + 2 are done from left to right, (8 − 3 + 2 = 5 + 2 = 7). Operations inside parentheses are done first, so parentheses can be used to override the priorities of the operations. Thus, (8 − 3) × 2 = 10.

Students must learn to be careful when using calculators. Although scientific calculators incorporate the order of operations, some simpler calculators do not. Simple calculators cannot store a long string of calculations, so they compute the operations in the order in which they are entered. Thus, a calculator that does not follow the conventional order would subtract first in solving the problem 8 − 3 × 2, giving the incorrect answer of 10. When using such a calculator, the user should enter the operations one at a time, in the order they should be performed.

To further develop children's number sense, the unit includes a lesson on divisibility rules (e.g., numbers divisible by five end in zero or five). By studying divisibility, students develop a better understanding of the operations of multiplication and division and how they relate to one another. Knowledge of the divisibility rules contributes to fluency with the multiplication and division facts. Students develop the rules themselves by identifying and describing patterns and then making generalizations that can be applied to other numbers. Although students may be acquainted with these ideas, discussing them gives students new tools for working with numbers and opportunities to generalize from patterns, which is an important algebraic skill.

Students began exploring multidigit multiplication at the end of Unit 4 when they developed both mental math and paper-and-pencil methods for one-digit by two-digit problems. Students continue their study of multiplication in this unit by first investigating patterns that occur when multiplying multiples of ten. They use rectangles, base-ten models, and break-apart strategies to explore these patterns and find products such as 3 × 20, 3 × 200, 30 × 200, etc. Working with these products allows students to develop number sense for the relative size of products resulting from multidigit multiplication. At the same time, facility with multiplying with multiples of ten is an important skill for mental math and estimation.

Students next move to computational estimation of products involving larger numbers. Because of their work with multiples of ten, students learn strategies of estimation that involve rounding to convenient numbers before multiplying. Working with estimation of products allows students to approach multidigit multiplication with an understanding of whether the results of their computations are reasonable. It also places an emphasis on mental math as a strategy for multidigit computations.

Estimation is treated alongside computation because both sets of skills are woven tightly together. The ability to estimate products supports efficient computation and vice versa. For example, students who are comfortable estimating a product such as 796 × 8 will be able to use estimation to check that a calculation is reasonable. Since estimation and mental math strategies are often both carried out by finding convenient numbers, good estimators become better at solving problems using mental math. Using the same example, a student who is comfortable estimating 796 × 8 as 800 × 8 may also be ready to calculate an exact product mentally, starting with 800 × 8. (800 × 8 = 6400; subtract 4 × 8 = 32 to get 6400 − 32 = 6368).

In this unit, particular attention is paid to identifying situations in which estimation can and should be used to solve problems. These include:

• checking the reasonableness of exact computations;
• finding a quick answer mentally when an exact answer is not required;
• computing when it is difficult or impossible to find an exact answer;
• calculating with numbers that do not stay the same over time; and
• calculating with numbers that are based on uncertain measurements.

For some problems, students are instructed to estimate. For others, they are left to decide whether to estimate or compute exactly and then explain the reasoning for their choice. Ultimately, students should be able to choose from mental math, paper-and-pencil methods, and estimation to solve problems.

A primary focus of this unit is to ensure that students have a conceptual foundation for the procedures they use to multiply multidigit numbers. To this end, students explore the underlying ideas, properties, and place-value concepts involved in multiplication. They do so using varied strategies and models for multiplication such as rectangles, coins, simpler-number methods, and numbers in expanded form. Students also develop paper-and-pencil strategies to improve efficiency, but they do so by using—and therefore maintaining—the conceptual connections among all of these methods.

Mental Math

By learning more than one strategy to solve computation problems, students become more flexible in their thinking and problem solving. They develop the power to choose and adapt strategies that help them solve problems more efficiently. Part of this efficiency results from the ability to solve problems using mental strategies when possible. The term mental math refers to any strategy that does not rely on a fixed computational algorithm, but that involves the flexible use of operations to simplify problems (e.g., modeling a problem with coins or thinking of 99 × 4 as 100 × 4 − 4). While mental math strategies lend themselves to efficient mental computation, they may still involve intermediate calculations on paper or use of manipulatives, particularly as students learn how to use the strategies (Verschaffel, et al., 2007, p. 566). Ultimately, an understanding of various methods and models they can use to multiply numbers serves as a tool to understand the mathematics behind each method more deeply, which leads to greater flexibility and efficiency in problem solving.

Models and Methods

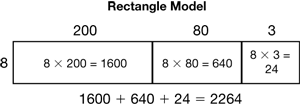
Figure 1 shows how this unit develops several strategies to create a learning progression through multidigit multiplication. Following this progression, the rectangular model helps students make sense of the expanded-form method. The all-partials method is then developed as a shorthand version of the expanded-form method. See Figures 2, 3, and 4. The compact method, which can otherwise become a series of unintelligible steps or “a black box” to students who lack a conceptual understanding of multiplication, has more meaning when it is connected to the all-partials method. See Figure 5.

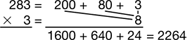
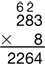
While the multiplication lessons in this unit do follow a progression similar to that shown in Figure 1, it does not mean that the compact method is always the end-goal, the best method, or even the most efficient strategy in all situations. Some students may find another method more efficient simply because they are much more likely to be accurate using it or because the numbers allow for the easy use of mental math strategies. As such, these methods can be seen as a series of interconnected strategies as shown in Figure 6. Each method sheds light on multiplication in a slightly different way. Because each helps develop a deeper overall understanding of the mathematical concepts and properties, proficiency with one supports proficiency with each of the others.

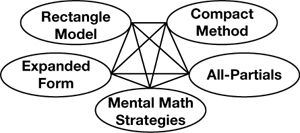
Therefore, it is important that students become comfortable making connections between the various methods for multiplication. For example, students who understand the all-partials method should be able to correlate it with a rectangle model to show where each of the partial products comes from as shown in Figures 2 and 4.

Developing a menu of varied strategies allows students to understand and make use of the place value concepts and number properties involved in multiplication. As students multiply using the expanded form, for instance, place value is highlighted as central to the process of multiplication. As a result, students learn that procedures for multiplying 283 x 8 do not involve multiplying “2 by 8,” but rather 2 hundreds by 8, or 200 by 8. Similarly, the expanded form emphasizes the role of the distributive property in multidigit multiplication, whereby each partition of 283 (200, 80, and 3) is multiplied by 8 as shown in Figure 3.

Practice

Practice is an essential part of mathematics. It is important for students to improve accuracy and efficiency with multidigit multiplication. Practice problems are included in the unit to build computational skills. Students should do these problems thoughtfully, using multiple methods, rather than rush through a page of calculations without checking for errors or considering the reasonableness of their answers. If students practice incorrect procedures, it is more difficult for them to learn correct ones (National Research Council, 2001).

Fluency with basic procedures enhances conceptual understanding of new material. It is achieved gradually over time and is maintained with regular and consistent practice. Students develop fluency with algorithms at different rates. Lack of fluency should not be a deterrent to moving on to different topics. In Math Trailblazers, computational practice is implemented according to the following considerations:

1. Practice is distributed over the curriculum. Students do short sets of problems frequently, rather than many problems all at one time, especially in the routines of Daily Practice and Problems and Home Practice.
2. Practice is embedded in problem solving in the lessons, activities, and games.
3. Opportunities for targeted practice are provided within a unit based on individual students' progress meeting Expectations.
4. Students practice material already mastered while learning new content.

This program of practice allows teachers to monitor students' use of computation strategies as they are being developed. Teachers can quickly identify incorrect procedures and help students correct them before they become ingrained.

This unit continues the review and assessment of the division facts to develop mental math strategies, gain fluency, and to learn to apply multiplication and division strategies to larger numbers. Students will focus on the division facts for the 2s and 3s.

Resources

• National Research Council. “Developing Proficiency with Whole Numbers.” In Adding It Up: Helping Children Learn Mathematics, J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
• Principles and Standards for School Mathematics. The National Council of Teachers of Mathematics, Reston, VA, 2000.
• Van de Walle, J. A. and Lovin, L. Teaching Student-Centered Mathematics: Grades 3–5. Pearson Education, Boston, 2006.
• Verschaffel, L., B. Greer, and E. De Corte. “Whole Number Concepts and Operations.” In Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics, Vol. 1 p. 566, Frank Lester, Jr., ed. Information Age Publishing, Charlotte, NC, 2007.