Lesson 6

Using Multiplication Strategies

Est. Class Sessions: 2

Developing the Lesson

Part 1: Strategies for Multiplying 2-Digit Numbers

X

A mental math strategy refers to any strategy that does not rely on a fixed computational algorithm. We use the term here to mean any strategy that involves the flexible use of operations to simplify problems (e.g., modeling a problem with coins or thinking of 99 × 4 as 100 × 4 − 4). While mental math strategies lend themselves to efficient mental computation, they may still involve some intermediate calculations on paper or modeling with manipulatives, particularly in the early stages of practice.

Mental Math Strategies.

Begin by asking students to solve 5 × 12:

X
  • Solve 5 × 12 using whatever strategy you choose.
  • Solve 5 × 12 using a mental math strategy.

Tell students a mental math strategy is one where they may break a problem into simpler problems. There are several ways to solve 5 × 12 using mental math:

  • Mentally break 12 into parts, 10 and 2. Then, 5 × 10 = 50 and 5 × 2 = 10; 50 + 10 = 60.
  • Double 5 to make 10; 10 × 12 = 120. Half of 120 = 60.
  • Use repeated addition and doubling. Double 12 to get 24, then double 24 to get 48; that makes 4 twelves, so one more 12 makes 60.
  • 5 × 11 is 55; one more 5 makes 60.
  • Five dimes is 50¢; 5 × 2¢ is 10¢; 50¢ + 10¢ = 60¢.

Have students read the opening vignette on the Using Multiplication Strategies pages in the Student Guide. Discuss the different strategies identified in the vignette. See the TIMS Tip.

Ask:

X
  • Describe the strategies in your own words.
  • Which students used mental math strategies? (everyone but Grace)
  • Which students used a paper-and-pencil method? (Grace)
  • Are there other strategies that can be used for any of the problems?
X

To help students describe the strategies in the Student Guide in their own words, assign student pairs one of the strategies. Each pair can write a short script for Nicholas, Jackie, Tanya, Luis, or Grace. The script will help one student in each pair explain the strategy to the class and should include the props (tools) that the student will need to represent the strategy. For example, Nicholas might use a display set of coins or Tanya might use markers on chart paper to draw the number line.

Pose additional problems that parallel those given in the vignette such as:
        27 × 3         10 × 73         49 × 6         5 × 64

Ask students to solve them with a partner and then share their strategies and decide which strategy they like best for each problem.

X

Note students' abilities to use place value concepts and mathematical properties to solve multidigit multiplication problems as they complete Check-In: Questions 1–3 in the Student Guide and discuss their methods [E3]. See the Workshop in Lesson 8 for targeted practice on this Expectation.

Have students answer Questions 1–3 and discuss whether everyone will choose to use the same method or strategy to solve a particular problem. The answer, of course, is that they probably will not.

As students explain, elicit further discussion by asking questions similar to the following:

X
  • Would you have used a different strategy than the students in the book used? For which problem? Why?
  • Is there a strategy that you use more than others? Why?
  • Do you use the same strategy or method for every multiplication problem?
  • Do you ever see a problem that you think might be easier to solve a different way? Can you give an example?
  • What makes a strategy fit one problem better than another?
  • “Thinking about money” is one strategy. Will that strategy work well for every problem? Why or why not? Can you give an example of a problem where it would work well? Can you give an example of a problem where another method would work better?

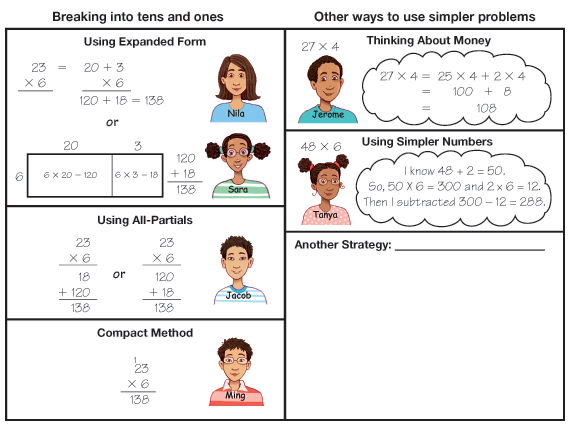
Paper-and-Pencil Methods. Have students refer to the Multiplication Strategies Menu in the Student Activity Book. See Figure 1. Ask students to compare the menu to the strategies the class has been collecting. Ask students to add strategies not represented in the blank space on their Multiplication Strategies Menus. Ask them to demonstrate strategies added.

Question 4 compares using the rectangle method with the expanded-form method that Grace used in the opening vignette to solve 5 × 22. The two methods are similar in that they both break 22 into 2 tens (20) and 2 ones before multiplying by 5 and then adding the two products (100 + 10 = 110). The rectangle method shows this using an area model. Question 5 asks students to solve problems using both methods and compare answers. Have them demonstrate their solution paths on a display or on the board. Half-Centimeter Grid Paper is provided in the Student Activity Book to help students organize their work.

X

Some students will need the support of a grid, while other students will be able to represent the problem with a simple rectangle.

X

Note students' abilities to make connections between expanded form and a rectangle model for multiplication using Check-In: Questions 4–5 in the Student Guide [E4]. The Workshop in Lesson 8 provides targeted practice on this Expectation.

Questions 6–8 discuss and compare the all-partials and the compact methods. Have students demonstrate and explain their solution paths for the problems in Question 8.

Question 9 underscores the fact that the order does not matter when using the all-partials method. That is, the same answer will be reached regardless of whether the tens or the ones are multiplied first. In Questions 10–12, students identify the partial products.

You may assign Questions 1–4 of the Homework section in the Student Guide at this point.

Student Guide: 279 280 281
Answers
X
SG_Mini
+
X
SG_Mini
+
X
SG_Mini
+
Student Activity Book:
Master:
Multiplication Strategies Menu
X
+