The break-apart products method for multiplication allows us to do many calculations mentally and is, in fact, the basis for the traditional paper-and-pencil multiplication algorithm. This lesson develops the method with larger numbers and lays the foundation for working with multiplication algorithms.
Research and our experiences in Math Trailblazers classrooms suggest that students who understand the concepts and methods developed in this lesson are more likely to develop and retain efficient multiplication methods. This means that they can choose and apply the most appropriate procedure for a given problem (e.g., mental math, paper and pencil, or estimation). Students who are asked to learn algorithms, such as the compact method, before they understand the underlying concepts and explore other strategies become inflexible and tend to use the same algorithm all the time instead of choosing to use mental math or other strategies when they are appropriate.
Find the Number of Squares. Show the display of Question 1 on the Exploring Break-Apart Products with Larger Numbers pages in the Student Activity Book. Ask students to work in pairs to find the number of squares in the 5 × 28 and 32 × 5 rectangles. As pairs work together, encourage them to use their own methods and you should note the strategies that they use. They will likely divide the rectangles into smaller rectangles and add the areas together.
- Did you break the rectangles into smaller rectangles to make it easier to find the total number of small squares? If so, how? (Possible response: For 5 × 28, I made a rectangle for 5 × 20 = 100 and one for 5 × 8 = 40. I added 100 + 40 = 140. For 32 × 5, I made a rectangle for 30 × 5 = 150 and one for 2 × 5 = 10. I added 150 + 10 = 160.)
- Which methods for breaking the rectangles into parts are more efficient?
Students may choose different ways to divide the rectangle into two rectangles. Efficient methods include, but are not limited to, the following:
- Breaking rows or columns into groups of five or ten, so students can skip count or use multiples of ten to find the total number of small squares.
- Dividing the rectangle in half, so they can use doubling to find the total.
Show or ask students to show the different ways to divide the rectangle using the display.
Use Rectangles to Find Products. Remind students of the work they did in Lesson 5 Break-Apart Products. Have them look at Question 2.
Use these prompts to set expectations for this question.
- Before you begin to answer Question 2, talk with your partner. Decide on the most efficient way to divide the rectangle into two parts.
- Work together to write the number sentences in the small rectangles as you did in Lesson 5 and then write a number sentence to find the total.
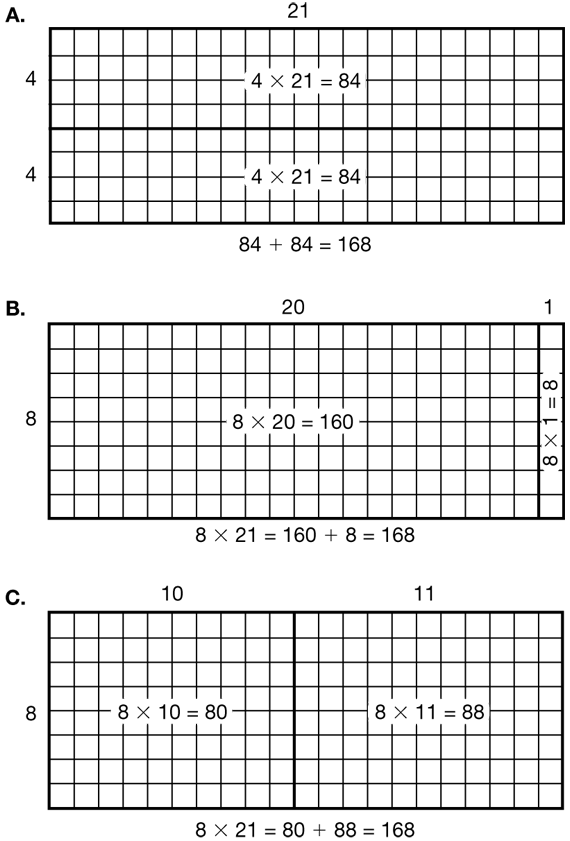
Ask pairs to show the class their solutions on a display and to justify their choice of partitions. Possible responses are shown in Figure 1. Compare the strategies and discuss which ways make the multiplication easier.
Sample work from classrooms shows that some students have misconceptions and make the errors described below:
- Students do not divide the rectangles at all and write one number sentence such as 8 × 21 = 168. Help students find ways to divide the rectangle to make the multiplication easier.
- Students do not write number sentences for the parts that match the smaller rectangles. Ask these students to match the numbers in the number sentences with the rows and columns.
- Students do not write a number sentence that shows the sum of the two parts. Ask these students how they can find the total number of squares and to write a number sentence that shows that they added the two parts together.
- Which ways to break products apart make it easier to find the answer? (Possible response: Breaking a factor so one of its parts is a multiple of 10 helps since it is easy to multiply by tens, as in Samples B and C. Breaking one factor in half helps too, since then we can double to get the answer, as in Sample A.)
- When can you break a factor in half? (When one of the factors is an even number like 3 × 12 or 4 × 26.)
Help students show their methods clearly using number sentences. Use discussion prompts similar to the following for the method shown in Sample A for 8 × 21 in Figure 1.
- How are the 8 rows divided into two parts? (in half—4 rows and 4 rows)
- How many squares are in each half? How do you know? (4 × 21 is 84 squares)
- Where is that number sentence written on the rectangle? (on each half)
- What does each number in the number sentence stand for? (4 rows times 21 squares in each row equal 84 squares in each half.)
- How many squares are there in the large rectangle? How do you know? (168 squares is 84 doubled. Add the number of squares in the two parts and you get the total.)
- What is that number sentence? (84 + 84 = 168 squares)
Use similar questions to discuss the number sentences in Sample B for 8 × 21 in Figure 1:
- How are the 21 columns divided into two parts? (into tens and ones—20 and 1)
- Where is that written on the rectangle? (on the top of the rectangles)
- How many squares are in each smaller rectangle? How do you know? (There are 8 × 20, or 160 squares in the first rectangle and 8 × 1, or 8 squares in the second rectangle)
- Where are those number sentences? (in each small rectangle)
- How many squares are there in the large rectangle? How do you know? (168 squares; add the number of squares in the two parts and you get the total.)
- What is that number sentence? (160 + 8 = 168 squares)
Ask students to complete Questions 3 and 4. As they work, help students show their strategies by clearly showing on the rectangles how they are divided and by writing number sentences that match their parts. See the Meeting Individual Needs box for a discussion of ways to address possible misconceptions and errors.
Assign the Practicing Break-Apart Products Homework pages in the Student Activity Book after Part 1.