Give each student at least 28 square-inch tiles.
Solve and discuss solutions to the following problems:
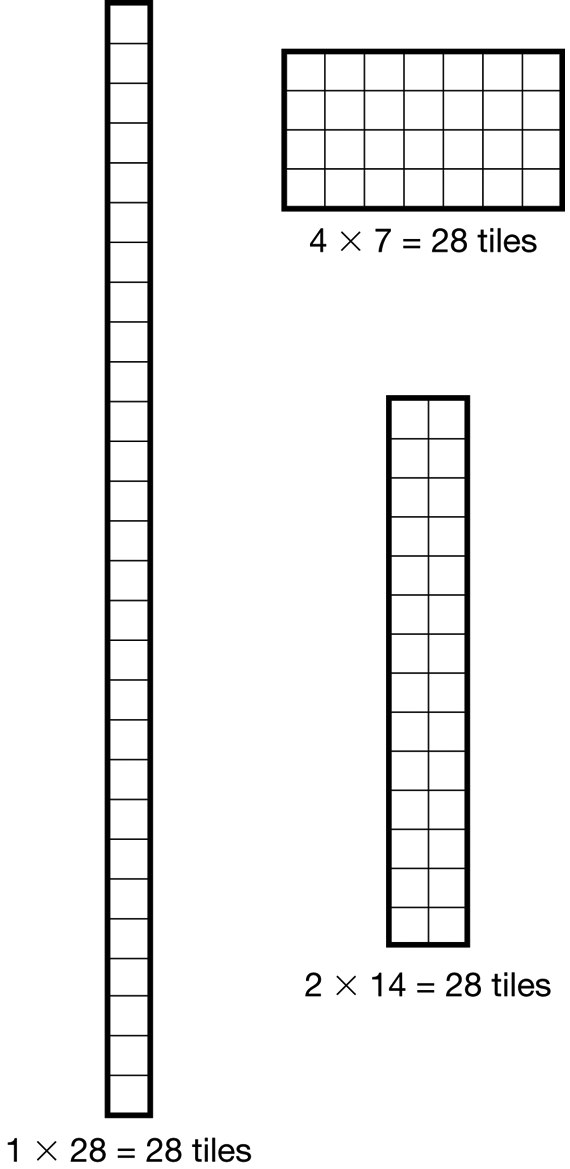
- Jacob has 28 square carpet tiles. He wants to put them together to make a rectangular rug to cover part of the den floor. He tries several arrangements. He seems to like the rug that has 4 rows. How many tiles are in each row? How do you know? (There are 7 tiles in each row. I used the tiles; I know 4 × 7 = 28; I know that 28 ÷ 4 = 7. See Figure 3.)
- What other ways can Jacob arrange 28 square carpet tiles into a rectangle? (Possible response: He can make a long rug that is 28 squares long, or 1 × 28. He can make another skinny rug that is 2 × 14; I used the square-inch tiles to figure out how many tiles are in 2 rows. I know 28 is a multiple of 2 because it is even.)
- Jacob wants the rug to cover the floor so he and his brother can play games and build forts. Which arrangement should he choose? Why? (Student answers will vary. Some students might reason that they want a long space, so the rug that is 2 × 14 makes sense. Other students will reason that a rug that is wider is better for the forts, so the rug that is 4 × 7 makes sense.)
- Is 28 a multiple of 4? How do you know? (Yes, 28 is a multiple of 4. I can line up four rows and use all 28 tiles to make a rectangle. 4 × 7 = 28)
- Is 28 a multiple of 3? How do you know? (No, 28 is not a multiple of 3. I cannot line up 3 rows and use all 28 tiles to make a rectangle. I have one left over.)
- Is 5 a factor of 28? How do you know? (No. 28 does not end in 5 or zero, so it is not a multiple of 5; When I try to build a rectangle with 5 rows, I need two more squares to make a rectangle.)
- Is 28 a prime number? How do you know? (No. 28 is not prime. 28 has more than 1 and itself as factors.)
- Is 28 a square number? How do you know? (No. 28 is not a square number. I cannot build a square with 28 pieces.)
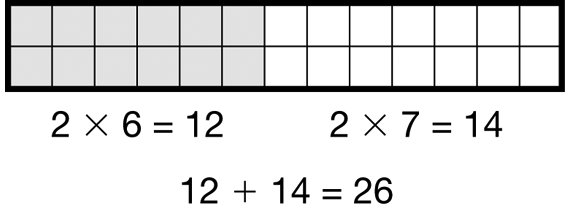
- Jacob decided to move the carpet squares to his room. The space where he wants the rug is 2 square tiles by 13 square tiles. How many square tiles does Jacob need to cover the space? Use the break-apart method to solve 2 × 13. (Strategies will vary. 2 × 10 = 20 and 2 × 3 = 6, so 20 + 3 = 26.)
Ask students to find another way to break apart the rectangle to solve 2 × 13. See Figure 4. While students are finding their solution, circulate through the classroom looking for students that are having trouble breaking apart the rectangle or putting the parts together.
Have several students share with the class their strategy for solving the problem. Draw several copies of the rectangle on a grid to help students share and compare their solutions. Watch for how confidently students break apart the rectangle.