Array Model of Multiplication

The first situation in which students encountered multiplication in third grade involved objects arranged in equal-sized groups, as in Figure 1. They learned that the number of objects in 5 groups of 6 objects is 5 × 6. The product can be found by repeated addition:
5 × 6 = 6 + 6 + 6 + 6 + 6.

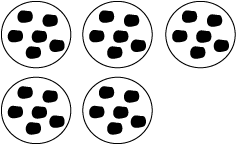
In this unit we look at arrays as another model for multiplication. An array is an arrangement of elements into a rectangular pattern of (horizontal) rows and (vertical) columns. For example, a candy box that contains 5 rows with 6 pieces in each row is a 5 × 6 array. The array model of multiplication is just a special case of the equal grouping model, where the rows of the array are the groups. Thus, the number of objects in 5 rows of 6 objects is 5 × 6. One virtue of the array model is that by rotating the array, one can see very clearly that 5 × 6 = 6 × 5—an example of the commutative property, or turn-around rule. Another advantage is that it creates a visual image of a multiplication problem. See Figure 2.

Just as many things naturally come in groups, there are many things that naturally come in arrays. For example, eggs in a carton, candy in a box, soda cans in a six-pack, panes in a window, and ice cubes in a tray all come in arrays. Recognizing arrays when they occur helps students recognize problems that can be solved by multiplication.

Distributive Property

In Lessons 5 and 10, Break-apart Products and Break-Apart Products with Larger Numbers, students solve multiplication problems by breaking products into the sum of simpler products. The fundamental property that is involved in this process is the distributive property. This property states that for any numbers a, b, and c,

For example, to multiply 7 × 4, we can partition 7 into two parts, 5 + 2. The problem then becomes (5 + 2) × 4. Applying the distributive property gives (5 × 4) + (2 × 4).

Students solve this problem by showing the problem as an array (or rectangle), and then partitioning the array.

20 + 8 = 28

This unit does not include formal instruction on the distributive property. However, the activities will help students develop an informal understanding of this property which will enable them to do many calculations mentally and is the basis for paper-and-pencil multiplication algorithms. In the example above, students can use known facts (5 × 4, 2 × 4) to find a harder fact (7 × 4).

Division

Two distinct types of division situations are encountered in this unit. In both types, a set of objects is divided into equal-sized groups. In equal sharing or partitive division, the number of groups (partitions) and the total number of objects in the set are known. The number in each group is found by division. For example:

• Twelve cookies were divided equally among four children. How many cookies did each child get? (12 ÷ 4 = 3)

Problems of this type can be solved by “dealing out” the objects to the groups.

In equal grouping or measurement division, the number in each group (the measure of the group) and the total number of objects in the set are known. Division is used to find the number of groups. For example:

• Twelve cookies were put onto plates, with three cookies on each plate. How many plates of cookies were there?

Problems of this type can be solved by making groups of a specific size and then counting the number of groups. This type of division is also known as subtractive because the process can be seen as repeated subtraction of a specific number.

Students need to be presented with examples of both types of division problems, although they do not need to identify them by name.

Prime Numbers

A whole number is a prime number if it has no factors other than itself and one. All other (whole) numbers larger than one are called composite numbers and can be expressed as products of prime numbers. In that sense, prime numbers are the building blocks from which all other whole numbers are multiplicatively made. Because of this, the prime numbers have been the subject of much study. Around 300 BCE, the Greek scholar Euclid proved that there are infinitely many prime numbers. Although there is no quick way to test whether a number is prime, computers have made it possible to produce long lists of prime numbers. However, there are many unanswered questions. A sample of the kinds of questions mathematicians ask about prime numbers includes the following:

Some pairs of prime numbers, such as 3 and 5, 11 and 13, and 29 and 31, are only two apart. These are called twin primes. Are there infinitely many twin primes? No one knows the answer.

Many numbers are the sum of a square number and a prime number. For example, 19 = 16 + 3 and 14 = 9 + 5. Is this true for all numbers from some point on? Again, no one knows the answer.

The distributive property is a generalized rule that applies regardless of the numbers being added or multiplied. As students use this property to solve numerical problems, they are developing early algebraic reasoning skills. The same is true for other properties explored in this unit as well. The multiplication properties of 0 and 1 state that any number times zero is zero and any number times one is the number itself. The commutative property of multiplication, or “turn-around rule,” states that changing the order of the factors does not change the product. As students apply these rules to solve multiplication problems, they develop the connection between computation and generalized algebraic properties.

This focus on early algebraic thinking is developed throughout Math Trailblazers. Following recommendations of researchers, activities that give students concepts and skills needed to make a natural transition from learning and doing arithmetic to learning and doing algebra are integrated through all grades. (Carpenter et al., 2003; Carraher and Schliemann, 2007; Kaput, 2008; Kilpatrick and Izsak, 2008; Schliemann et al., 2007). Students extend and connect their concepts of number, geometry, measurement, and data to develop tools for algebraic reasoning. These tools enable them to “do algebra,” that is, to identify, describe, visualize, and simplify patterns and relationships. They learn to generalize procedures they use for arithmetic. They also learn to make generalizations about numbers that are collected in data sets, organized in tables, and pictured in graphs.

The goal of the math facts development in Math Trailblazers is for students to learn the basic facts efficiently, gain fluency with their use, and retain that fluency over time. A large body of research supports an approach in which students develop strategies for figuring out the facts rather than relying on rote memorization. This not only leads to more effective learning and better retention, but also to the development of mental math skills. In fact, too much drill before conceptual understanding may interfere with a child's ability to understand concepts at a later date. The research that contributed to the National Council of Teachers of Mathematics Principles and Standards for School Mathematics and the National Research Council's Adding It Up has informed the structure of the math facts strand in Math Trailblazers. Also see the Unit 3 Letter Home for more about the development of the basic facts in 4th-Grade Math Trailblazers.

Multiplication Facts

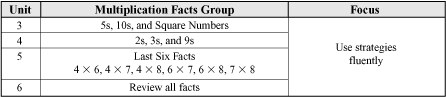
This unit begins a systematic review and assessment of the multiplication facts to develop mental math strategies, gain proficiency, and to learn to apply multiplication strategies to larger numbers. Students study small groups of facts that can be solved using similar strategies. See Figure 1.

Resources

• Bennett, Albert B., Jr. and L. Ted Nelson. Mathematics for Elementary Teachers: A Conceptual Approach. McGraw Hill, Boston, 2001.
• Carpenter, T.P., M.L. Franke, and L. Levi. Thinking Mathematically. Heinemann, Portsmouth, NH, 2003.
• Carraher, D.W. and A.D. Schliemann. “Early Algebra.” F.K. Lester, Jr., ed. Second Handbook of Research on Mathematics Teaching and Learning. Information Age Publishing, Inc., Charlotte, NC, 2007.
• Kaput, J.J. Algebra in the Early Grades. Lawrence Erlbaum Associates, New York, NY, 2008.
• Kilpatrick, J. and A. Izsak. “A History of Algebra in the School Curriculum.” C.E. Greens and R. Rubenstein, eds. Algebra and Algebraic Thinking in School Mathematics. The National Council of Teachers of Mathematics, Reston, VA, 2008.
• National Research Council. “Developing Proficiency with Whole Numbers.” In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
• Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, Reston, VA, 2000.
• Schliemann, A.D., D.W. Carraher, and B.M. Brizuela. Bringing Out the Algebraic Character of Arithmetic. Lawrence Erlbaum Associates, Publishers, Mahwah, NJ, 2007.
• Smith, John P. and P. Thompson. “Quantitative Reasoning and the Development of Algebraic Reasoning.” Algebra in the Early Grades, Jo Kaput, D. Carraher, M. Blanton, eds. Lawrence Erlbaum Associates, New York, NY, 2008.