Use Arrays to Show Fact Families. Begin this lesson with a discussion of fact families. Your students may remember working with fact families in Grade 3.
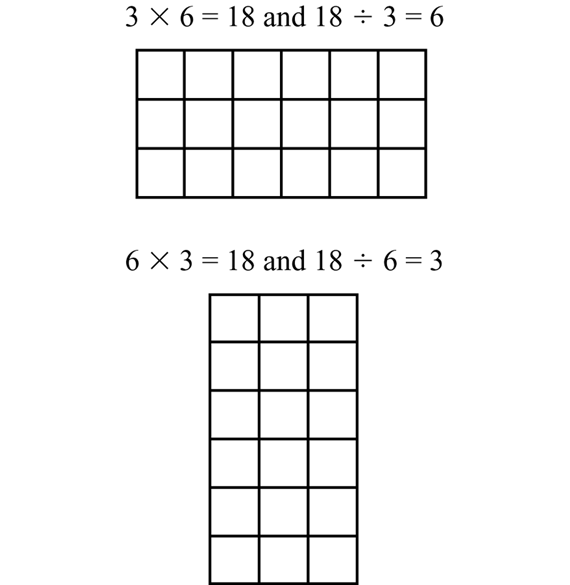
Using a rectangular array, review with students what a fact family is. If a number sentence matches a rectangle, then all the number sentences in that fact family also match the same rectangle. Use Linda and Ming's arrays on the Fact Families pages in the Student Guide and model them with square tiles or with a display of Square-Inch Grid Paper from Lesson 1. Show both vertical and horizontal representations. See Figure 1.
- What are the two multiplication sentences for this array? (3 × 6 = 18 and 6 × 3 = 18)
- What do you know about those multiplication sentences? (They are in the same fact family.)
- What are the two other facts in this same fact family? (18 ÷ 3 = 6 and 18 ÷ 6 = 3)
- Can you use this array to show those two division facts? (Taking the total of 18 square-inch tiles and dividing them into 3 equal rows leaves 6 in each row, 18 ÷ 3 = 6; do the same for 18 ÷ 6 = 3.)
Questions 1–4 in the Student Guide elicit the four number sentences for this rectangle. Have a student demonstrate how each number sentence in the fact family matches the rectangle.
For Question 5, students discuss a rectangle for 3 × 8 = 24. Have students draw the rectangle and ask questions to highlight the connections between the number sentences and the rectangle.
Questions 6–7 investigate fact families for square numbers. These fact families have only two number sentences since there is only one multiplication sentence and one division. For example, “turning around” the factors in the sentence 2 × 2 = 4 produces the same number sentence.
Question 8 calls attention to the difference between 5 × 2 and 52. Students write fact families for 5 × 2 = 10 and 5 × 5 = 25 (52).
Connect Multiplication and Division. The basketball vignette in the Using Fact Families section of the Student Guide presents a situation that illustrates the relationship between two facts (30 ÷ 5 = 6 and 5 × 6 = 30). Have student pairs read the story to each other. Discuss fact families and how they can be used to find a division fact when a multiplication fact is known. Students should see that division is the opposite (inverse) operation of multiplication.

Division. The basketball story is an example of partitive (equal sharing) division. See the discussion in Mathematics in this Unit in the Teacher Guide. The total is 30 and the number of groups (parts) is known—5 schools—but not the number of balls that will be in each group. To find out how many basketballs are in each group, a “dealing out” method is appropriate. There will be 6 basketballs in each group. 30 ÷ 5 = 6.
Question 9 gives an example of measurement (subtractive) division. The total number of soccer balls is 30 and the store is giving out crates of 6 soccer balls to as many schools as possible. The size (measure) of the groups is known, but not the number of groups. The answer (quotient) can be reached by repeated subtraction: 30 − 6 = 24; 24 − 6 = 18; 18 − 6 = 12; 12 − 6 = 6; 6 − 6 = 0. We subtracted 5 times so there are 5 groups. 30 ÷ 6 = 5.
The labels for these two situations are not important here. However, it is important for students to have opportunities to solve both types of problems.
Division Symbols. There are several different symbols that are commonly used to denote division. The quantity “32 divided by 4” can be represented as:
| (a) 32 ÷ 4 = 8 |
(b) 32/4 = 8 |
| |
| (c) 32/4 = 8 |
(d) 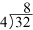 |
Each of these sentences can be read as “32 divided by 4 is 8,” “4 divided into 32 is 8,” “4 goes into 32 eight times,” or “there are 8 fours in 32.” It is important that students learn to read and write division sentences properly. The order of the numbers does make a difference. A common mistake, for example, is to read the division in (d) as “4 divided by 32.” But, “4 divided by 32” is 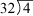 whose value is 32/4 or 1/8. In Math Trailblazers, we use 48 a variety of methods for displaying division sentences. Exposure to a variety of methods and symbols will prepare students for different experiences with division.
whose value is 32/4 or 1/8. In Math Trailblazers, we use 48 a variety of methods for displaying division sentences. Exposure to a variety of methods and symbols will prepare students for different experiences with division.

In Units 3–5, students use the Triangle Flash Cards and the Facts I Know charts only with the multiplication facts. They will build strategies for the division facts in Units 3–5 and use the Triangle Flash Cards to develop fluency with the division facts beginning in Unit 10. Reviewing the multiplication facts will facilitate their work with the division facts. Students will use the same groups of flash cards when they study the division facts.
Because the math facts program is closely linked to the recommended schedule for teaching lessons, classrooms that differ significantly from the suggested pacing will need to make accommodations in order to ensure that students receive a consistent program of math facts practice and assessment throughout the year.
Discuss Question 9 in the Student Guide.
- What information is given in the problem? (The total number of soccer balls, 30, and the number of balls in each group, 6.)
- What does the answer, the quotient, tell you? (The number of schools that will receive soccer balls.)
- How is Question 9 different from the basketball story? Think about what the problem tells you and what you need to find out. (In the story we know the number of schools, 5, and we want to find out the number of basketballs for each school, 6. In Question 9 we know the number of soccer balls each school will receive, 6, and we want to know how many schools will receive them, 5.)
- What number sentence represents the basketball story? (30 ÷ 5 = 6; using labels: 30 balls ÷ 5 schools = 6 balls per school)
- What is a number sentence for the soccer ball problem? (30 ÷ 6 = 5; using labels: 30 balls ÷ 6 in each group = 5 schools)
- How are they alike? (They have the same numbers. Thirty is the dividend in both sentences.)
- How are they different? (The divisors and quotients change. Thirty basketballs are divided into five groups in the basketball story. Thirty soccer balls are divided into groups of six balls each in the soccer ball problem.)
- How can we check a division problem? Give me an example. (Multiply the quotient by the divisor. To check 30 ÷ 6 = 5, multiply 5 times 6 to get 30.)
- What can we say about multiplication and division together? (They are opposites. They “undo” each other.)
- What are the four number sentences in this fact family? (5 × 6 = 30; 6 × 5 = 30; 30 ÷ 5 = 6; 30 ÷ 6 = 5)
Remind students that the two multiplication sentences are turn-around facts (5 × 6 = 30 and 6 × 5 = 30).
Ask students to work through Questions 9–25 in pairs. Questions 14–25 provide practice with fact families. Some are in the context of money. These questions can also be assigned for homework.
Multiply with 0 and 1. Have students complete Questions 26–29 in pairs before discussing them together as a class.
- How can both 18 × 0 and 9 × 0 equal the same answer? (Possible response: eighteen groups of zero objects and nine groups of zero objects are both zero.)
- Make up a number story about Question 28D. (One possible story: Jackson's Hardware Store gave away one box of ten table tennis balls. How many balls did the store give away?)
- What is one times ten million? How do you know? (Ten million. One group of ten million is just ten million.)
- What is the product of one and any number? How do you know? (That number. Because one group of any number is that number.)
- What is zero times ten million? How do you know? (Zero. If I have zero groups of ten million balls, I have zero balls.)
- What is the product of any number and zero? How do you know? (Zero. Repeated addition of zero any number of times is zero and zero groups of any number is still zero.)

This lesson illustrates the following mathematical properties:
Multiplication Properties of 0 and 1.
- Any number times zero is zero. Using variables, n × 0 = 0.
- One times any number is that number. Using variables, n × 1 = n.
Commutative Property of Multiplication. Changing the order of the factors does not change the product. For example, 3 × 5 = 5 × 3 = 15. Using variables, n × m = m × n. See Lesson 1.
It is not necessary at this point that students know the names of these properties or be able to state them using variables. It is sufficient that they can use the ideas when they solve problems.
After completing the discussion of Questions 26–29, assign Check-In: Questions 30–33 to students to complete independently.
Use Check-In: Questions 30–33 in the Student Guide to note students' progress toward solving multiplication problems using 0 and 1 as factors (applying the multiplication properties of 0 and 1) [E7], and using turn-around facts to solve multiplication problems (applying the commutative property of multiplication) [E8].
Multiplication Facts and Triangle Flash Cards. The Multiplication Facts and Triangle Flash Cards section in the Student Guide outlines how students use the Triangle Flash Cards for multiplication, and Part 1 of Home Practice provides a quick review.
Have students read through the directions in pairs. They may recall working with Triangle Flash Cards in third grade. Take this opportunity to remind students to use the terms product and factor when talking about multiplication and division problems.













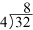
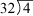 whose value is
whose value is