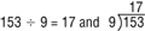Solve Tile Problems. Ask students to work in pairs to complete Questions 1–5 in the Tile Problems and Factors section on the Factors pages in the Student Guide. Student pairs should have square-inch tiles or copies of the Square-Inch Grid Paper Master from the Teacher Guide.
After students have completed their work, use the following prompts to guide a discussion.
- What number sentence can you write to describe the rectangle you made for Question 1? (6 × 5 = 30)
- What number sentence describes the rectangle you made using 21 tiles in Question 2? (21 ÷ 7 = 3)
- What other number sentences can you write that describe the rectangle you made in Question 2? (21 ÷ 3 = 7; 3 × 7 = 21; and 7 × 3 = 21)
- What number sentence describes the rectangle you made using 32 tiles in Question 3? (32 ÷ 4 = 8) What are the other number sentences that describe this rectangle? (32 ÷ 8 = 4; 4 × 8 = 32; and 8 × 4 = 32)
- For Question 4, what other rectangles did you make using 32 tiles? (Possible responses include a rectangle with 2 rows of 16 tiles (or 16 rows of 2 tiles) or a rectangle with 1 row of 32 tiles (or 32 rows of 1 tile).)
- How many tiles of each color did you find in Question 5? (There would be 4 tiles of each color.) What number sentence can you write to show this? (12 ÷ 3 = 4 or 3 × 4 = 12)
Define Factors. After discussing the problems, have students read together the definition of factor that follows the questions. This definition uses the two sides of a rectangle to define the factors of the total number of tiles and is the first of two definitions for factor given in this lesson. Have students answer Questions 6–8 in conversation with a partner.
The More Tile Problems part of the Homework section in the Student Guide can be assigned at this time. Square-Inch Grid Paper from the Teacher Guide should be sent home with these problems.
Use Rectangular Arrays. Before asking students to read the Finding Factors section on the Factors pages, discuss the topic of factors. Tell students that a number is a factor of another number if it divides evenly into the number; that is, if the answer is a whole number. This is the same as saying a factor is one side of a rectangle made with a total number of tiles. Factors can also be described as the whole numbers that can be multiplied together to get a number.
Ask the class the following questions:
- Can you arrange ten tiles into two equal rows? (Yes)
- Can you answer this without using tiles? (I think of 5 tiles in 2 rows. 5 × 2 = 10)
- How many tiles will be in each row? (5 tiles)
- What operation can be used to answer this question? (Students may suggest either a multiplication sentence, 2 × ? = 10, or a division sentence, 10 ÷ 2 = ? Either sentence describes the problem accurately and fully.)
- Can you arrange nine tiles into two equal rows? Give a division sentence to explain your answer. (There would be 9 ÷ 2 = 41/2 tiles in each row. That is not possible unless you cut the tiles, which is not allowed here.)

Most students see fairly quickly the connection between an array of tiles and a division sentence. However, others will need additional visual and tactile experiences with arrays of tiles before they are comfortable going directly to the division sentences and checking with calculators. Pose additional sample problems such as those below. Ask students to model them with square-inch tiles, name the factors, and give number sentences. Have them check with calculators to verify the factors.
- Can you arrange 8 tiles into 4 rows? into 3 rows? 2 rows?
- Can you arrange 14 tiles into 2 rows? into 3 rows? 4 rows?
- Can you arrange 15 tiles into 2 rows? into 3 rows? 4 rows?
- Can you arrange 16 tiles into 2 rows? into 3 rows? 4 rows?
The answers to the above questions show that 2 is a factor of 10, but it is not a factor of 9.
Refer students to the rectangles chart of the numbers 1–25 that they made in Lesson 1. Ask a student to select one number from the chart and identify its factors.
For example, if a student selects the number 15, ask:
- Name one factor of 15. (Possible response: 3)
- What tells you that 3 is a factor of 15? (The rectangle that has 3 on one side and 5 on the other side)
- How does that tell you that 3 is a factor of 15? (If I divide 15 into 3 rows, I get 5 in each row. All the rows have the same number of tiles. 5 is a whole number, not a fraction.)
- What is a number sentence that matches the rectangle? (3 × 5 = 15 and 15 ÷ 3 = 5)
- If 3 is a factor of 15, what does that tell you about 5? (5 is also a factor, because when I make 5 rows there are 3 in each row and 3 is a whole number.)
Use Calculators. Tell students that using a calculator is another way to find the factors of a number. Ask for a few more demonstrations of how to name the factors of a number using the class rectangles chart.
Calculators help students focus on finding patterns in multiples and factors while working with larger numbers and with factors they may not know easily.
Ask students to check 10 ÷ 2 and 9 ÷ 2 with their calculators. For the first question, they will get 10 ÷ 2 = 5. Two and 5 are both factors of 10 because they divide evenly into 10 and they are two whole numbers multiplied together to get 10.
For the second question, they will get 9 ÷ 2 = 4.5. This is not a whole number so 2 is not a factor of 9.
Have students use their calculators to answer the following:
- Can 51 tiles be divided evenly into 3 rows? What is the number sentence? (Yes, 51 ÷ 3 = 17 or 3 × 17 = 51.)
- Describe a rectangle that shows this. (3 rows with 17 tiles in each row)
- Is 3 a factor of 51? How do you know? (Yes, 3 is a factor of 51. Three divides 51 evenly, and 3 and 17 are two whole numbers that equal 51 when multiplied together.)
- Can 44 tiles be divided evenly into 8 rows? What is the number sentence? (No, 44 ÷ 8 = 5.5)
- Can you make a rectangle with 44 tiles and 8 rows? (No, 4 rows would have 6 tiles and 4 rows would have 5 tiles, so it wouldn't be a rectangle.)
- Is 8 a factor of 44? (No; 8 doesn't divide 44 evenly; 44 ÷ 8 = 5.5; 5.5 is not a whole number; also, you can't make a rectangle with 8 rows.)
- Can 156 tiles be divided evenly into 9 rows? What is the number sentence? (No, 156 ÷ 9 = 17.33333... Nine does not divide 156 evenly, since 17.33333... is not a whole number. Nine is not a factor of 156.)
- Can 153 tiles be divided evenly into 9 rows? What is the number sentence? (Yes, 153 ÷ 9 = 17, 9 × 17 = 153. 9 divides 153 evenly. Nine and 17 are two whole numbers that equal 153 when multiplied together, so 9 is a factor of 153.)

Use both ways of showing division in your discussions with your students so they get used to seeing both representations.
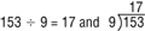
Have students read the vignette in the Finding Factors section of the Factors pages in the Student Guide. It includes the second definition of factor in which factor is defined in terms of the multiplication and division operations alone without reference to the rectangle model. The term multiple is also defined. Pose a few more multiplication number sentences and ask students to identify the factors and multiples.
Students then complete Questions 9–13 in the Student Guide. These questions can be completed independently, with a partner, or in a small group.