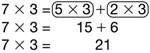Lesson 5

Break-Apart Products

Est. Class Sessions: 2

Developing the Lesson

Part 3. Writing Number Sentences for Break-Apart Products

X

The Distributive Property. The fundamental property that is involved in breaking apart products is the distributive property. (See the Mathematics in this Unit section.) Informal understanding of this property is very important for students—it helps them develop facility with mental math and prepares them to understand the traditional multiplication algorithm. Although formal study at this stage is not necessary, making connections between the arrays and number sentences will help students develop algebraic reasoning.

Ask students to turn to the Writing Number Sentences for Break-Apart Products pages in the Student Activity Book. Display the first page for the class. Have them complete Question 1.

Tell students they are going to write number sentences that represent the break-apart products the way mathematicians do, with number sentences. Ask students to work with a partner to complete Question 2 before asking a volunteer to complete the number sentences on the board.



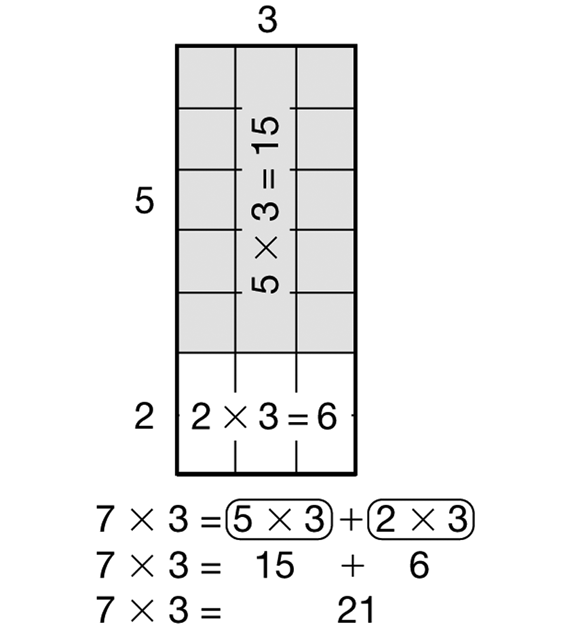
Ask questions to help students connect the number sentences with the picture. As students answer the questions, have them point to the picture to illustrate their thinking. See Figure 3.

Ask:

X
  • What does the 7 × 3 tell you about the picture? (The 7 tells the number of rows in the large rectangle and the 3 tells the number of squares in each row.)
  • What part of the picture does the 5 × 3 in the first circle represent? (5 × 3 represents the shaded rectangle.)
  • What do the 5 and 3 tell you about the rectangle? (The 5 tells the number of rows and 3 tells the number of columns or the number of squares in each row.)
  • What part of the picture does the 2 × 3 in the other circle represent? (2 × 3 represents the unshaded rectangle.)
  • What do the 2 and 3 tell you about the unshaded rectangle? (The 2 tells the number of rows and 3 tells the number of squares in each row.)
  • Where did the 15 and 6 come from? What do they tell about the rectangles? (The 15 is from 5 × 3 and it tells how many squares are in the shaded rectangle. The 6 is from the 2 × 3 and it is the number of squares in the unshaded rectangle.)
  • Where did the 21 come from? What does it tell about the picture? (The 21 is the sum of 15 and 6 added together. It is the number of squares in the large rectangle.)

Tell students that mathematicians use parentheses to show which operation to complete first. Show them how to rewrite the first sentence with parentheses. Students complete similar number sentences in Questions 3 and 4.

X

Using Parentheses. The agreed-upon rules for the order in which to perform operations say:

  • Do all the operations in parentheses first.
  • Then, do all the multiplications and divisions from left to right.
  • Then, do all the additions and subtractions from left to right.

    • In the expression (5 x 3) + (2 x 3), the parentheses are not needed, since the multiplication of 5 x 3 and 2 x 3 would be completed first whether or not the parentheses are written. However, the parentheses help students make sense of the number sentence.

    If students have trouble understanding which operation to complete first, ask them to circle the parts of the number sentence in parentheses, and complete those operations first.

Student Guide:
Student Activity Book: 59 60
Answers
X
SAB_Mini
+
X
SAB_Mini
+
Master:
Connecting number sentences and rectangles for break–apart products
X
+