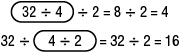Multiplying More Than Two Factors
Est. Class Sessions: 1Developing the Lesson
Part 1: Grouping Factors
Group and Order. Begin the lesson by discussing the example illustrated in the picture on the first Multiplying More Than Two Factors page in the Student Guide. There are 3 × 4 × 5 apples in a crate with 5 layers and 3 rows of 4 in each layer. Write the problem 3 × 4 × 5 on the board.
Students work with partners to answer Question 1 in the Student Guide.
After several minutes, ask:
After one group shows how they solved the problem, ask:
Have one or two more students share their methods. Remind students about the turn-around rule (commutative property) in which the order of numbers to be multiplied does not affect the answer. See Content Note in Lesson 1.
Ask:
Have students check the examples shown in the Grouping and Ordering section to see if they match the solutions they came up with as a class.
In small groups, ask students to discuss Question 2. After several minutes, ask them to share their group's responses with the whole class. This question introduces students to the associative property of multiplication. Students may refer to this property as the “grouping rule.” See Content Note.
Introduce the use of parentheses to “group” factors to show which ones to multiply together first. If students are more comfortable circling numbers, allow them to continue to do so. Use of parentheses will be discussed more formally in future units.
Associative Property of Multiplication. The associative property of multiplication is similar to the commutative property of multiplication in that they are both basic properties describing ways numbers can be manipulated to solve problems. The associative property says that when there is a string of numbers to be multiplied, such as 4 × 5 × 6, the answer will not be affected by grouping the numbers in different ways. For example, one can solve the above problem by grouping the 4 and 5 together first (20), and then multiplying that product by the third number to get 120.
4 × 5 × 6 = (4 × 5) × 6 = 20 × 6 = 120
Alternatively, the problem can be solved by grouping the 5 and 6 together first, multiplying (30), then multiplying that product by 4. Using either grouping results in the same answer, 120.
4 × 5 × 6 = 4 × (5 × 6) = 4 × 30 = 120
It is often helpful for students to understand the properties if they see counter examples. Ask students if you can change the grouping when dividing. Try:
Grouping matters when you divide.
The commutative property says that changing the written order does not matter. 4 × 5 × 6 will yield the same answer as 5 × 4 × 6, as well as 6 × 5 × 4. Naming the properties is not the important idea. Students can use “turn-around rule” to refer to the commutative property and “grouping rule” to refer to the associative property. It is important that students understand how to use them to solve problems.
Point out to students that they can choose groupings to make calculations easier. For example, Arti's method of solving 3 × 4 × 5 as 3 × (4 × 5) may lead to an easier mental calculation than David's or Lin's method.
Ask students to answer Questions 3–4 with partners. After students have completed most or all of the problems, select two or three problems to discuss with the whole class. Have students share their reasoning.
In Question 4, students find products of 3 factors using mental math, calculators, or multiplication tables.
Read and discuss with the whole class Jessie's and Frank's solutions to the multiplication problems presented on the page. These examples show how the turn-around rule and grouping strategies can be used to find products using mental math. Frank's solutions also show how to use the turn-around rule to mentally multiply by numbers that are multiples of 10.
Question 5 asks students to find ways to group or reorder the factors to make the problem easier for solving with mental math. Different students will find different groupings easier. Ask students to explain how they used mental math to solve each problem and explain why they grouped the factors in the way they did. Have students compare their different strategies.
