Lesson 5

Break-Apart Products

Est. Class Sessions: 2

Developing the Lesson

Part 1. Exploring Break-Apart Products

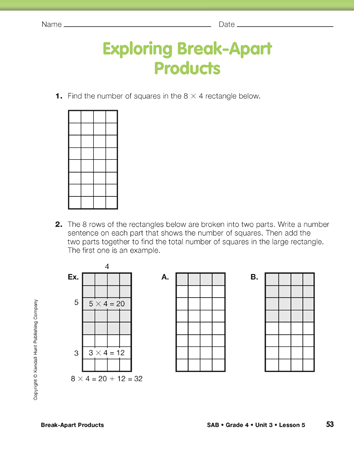
Use Rectangular Arrays to Find Products. Display Questions 1 and 2 on the Exploring Break-Apart Products pages in the Student Activity Book. Ask students to find the number of small squares in the rectangle in Question 1.

Ask:

X
  • What multiplication problem does this rectangle represent? (8 × 4)
  • How do you know? (There are eight rows. Each row has 4 squares.)

Give students a minute to solve the problem in pairs.

Then ask:

X
  • How much is 8 × 4? (32)
  • What strategies did you use to find your answer? (Possible strategies include: counting all the little squares; counting by eights: 8, 16, 24, 32; doubling 8 to get 16, then doubling 16 to get 32; knowing that three eights is 24 and one more eight is 32.)

Some students might say, “I didn't use a strategy—it is one of the facts that I just know.”

If so, ask:

X
  • Pretend that you have to help a friend who has a hard time remembering 8 × 4. How can you help? What strategy can you show your friend?

Model Break-Apart Products with Rectangular Arrays. Students explored the break-apart method in Grade 3, so some students might share this strategy. If so, ask them to demonstrate the strategy using the 8 × 4 rectangle.

If no one suggests a break-apart strategy, then explain that one way to solve a problem is to break it into smaller parts that are easier to solve.

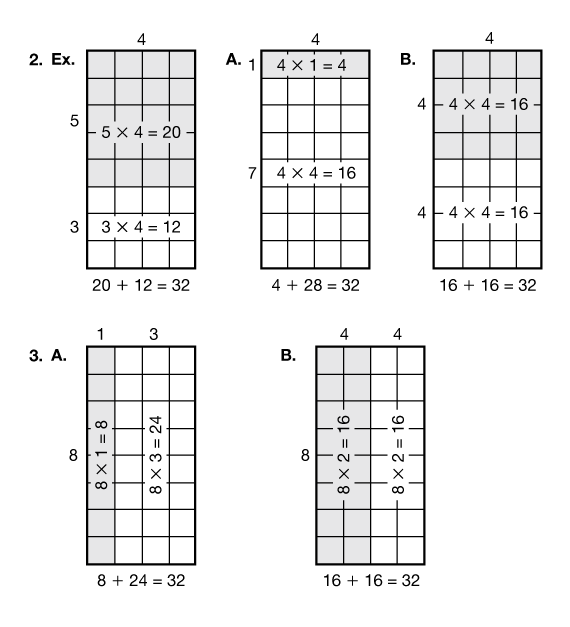
Use the example in Question 2 to model this strategy. This rectangle is broken into two smaller rectangles as shown in Figure 1, a 5 × 4 rectangle that is shaded and a 3 × 4 rectangle that is not shaded.

Use the following discussion prompts:

X
  • How are the 8 rows divided into two parts? (into 5 rows and 3 rows)
  • How many squares are in the shaded rectangle? (20 squares)
  • What do the numbers in the number sentence on the shaded rectangle stand for? (5 rows × 4 squares in each row = 20 squares.)
  • How many squares are in the rectangle that is not shaded? What do the numbers in that number sentence stand for? (3 rows × 4 squares in each row = 12 squares.)
  • How many squares are there in all? (32) How do you know? (Add the number of squares in the two parts and you get the total, 20 + 12 = 32.)

Ask students to work with their partners to explore other ways to break an 8 × 4 rectangle into parts by completing Questions 2–3. Discuss their results. See Figure 1.

Ask:

X
  • Which ways to break apart the 8 × 4 rectangles made it easier to find the answer to 8 × 4?

Responses will vary to the question above. Choosing ways to break apart a product so that the numbers are easy to multiply simplifies the multiplication process. For example, choosing the break-apart strategy for the example in Question 2 is an efficient strategy. Since most students know their fives multiplication facts, they will likely know that 5 × 4 = 20 and adding 20 to 12 is easy to do with mental math. Using doubles as for the rectangles in Questions 2B and 3B is also a strategy students frequently choose.

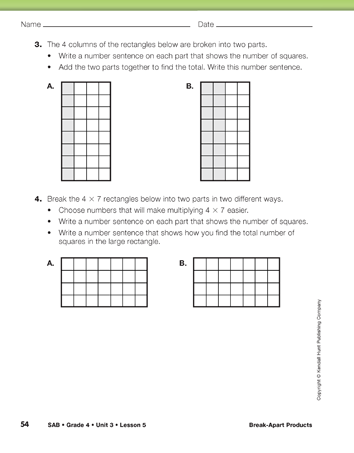
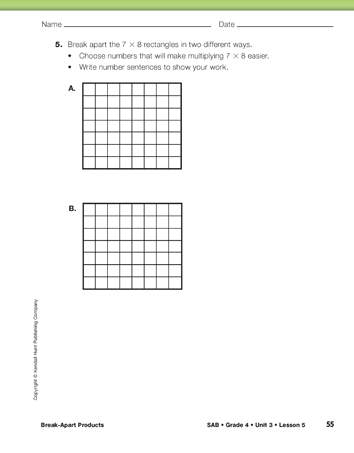
Ask students to work in pairs to complete Questions 4–5.

As they work, ask:

X
  • How can you break the rectangle into smaller rectangles to make the multiplication easier?

Remind students to write a multiplication sentence on each smaller rectangle to show the number of squares in each part.

Ask:

X
  • How can you use the number sentences for the smaller rectangles to show the total number of squares in the large rectangle? (You can add the products for the two smaller rectangles to find the total product.)

Have students share their choices for breaking the rectangles into two parts with the class. Discuss which ways make the multiplication easier.

X

To help students think about ways to break apart the rectangles, ask questions that help them think about the possible ways to break the factors apart. For example, for Question 5 ask:

  • One way to break 7 into two parts is 1 + 6 = 7. What are other ways to break apart 7? (2 + 5, 3 + 4)
  • Think about multiplying those parts by 8. Which facts do you know? (Possible response: 2 × 8 is easy and so is 5 × 8)
  • Where would you break apart the rectangle if you use 2 and 5? Show me on your rectangle.
  • How can you break apart 8? (1 + 7, 2 + 6, 3 + 5, 4 + 4)
  • Try multiplying those parts by 7. Which ways are easy for you?
Student Guide:
Student Activity Book: 53 54 55
Answers
X
SAB_Mini
+
X
SAB_Mini
+
X
SAB_Mini
+
Master:
Responses to Questions 2 and 3 on the Exploring Break-Apart Products page
X
+