Make Rectangles with 12 Tiles. Questions 1–6 on the Multiplication and Rectangles pages in the Student Guide provide a summary of the steps described in this section. You may prefer, however, to introduce the activity without these questions.
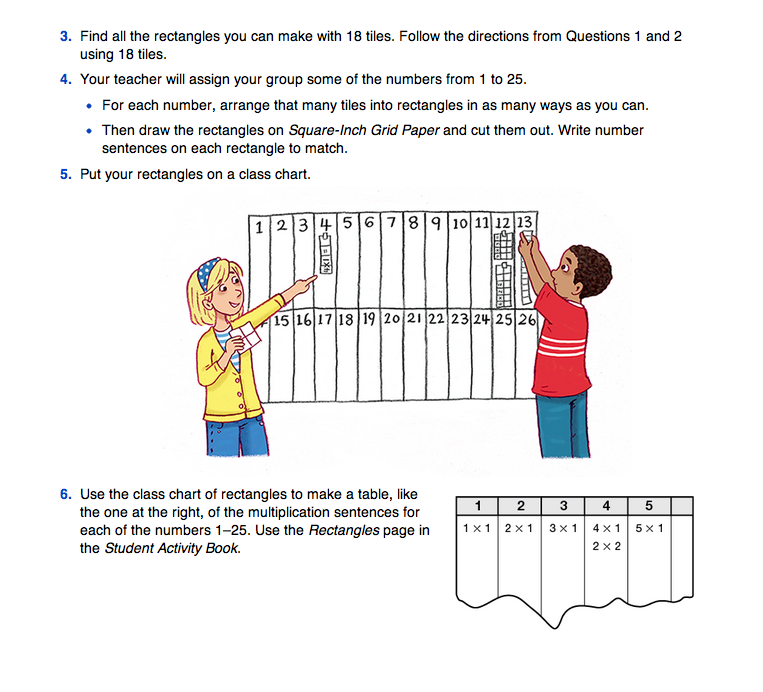
Distribute 50 tiles to each group of three to four students. Question 1 asks students to make rectangles using 12 square-inch tiles. See Figure 1. Establish with students that a “row” refers to the tiles going across. Tell them this is called an array—an arrangement of objects (in this case, square-inch tiles) in rows of equal length.
Ask a group to describe one of their rectangles:
- What is the area of one of the rectangles you made? (12 square inches, regardless of the shape)
- How many rows are in your rectangle?
- How many tiles are in each row?
Have students make this rectangle with their tiles while you make the same rectangle with a display that the class can see.
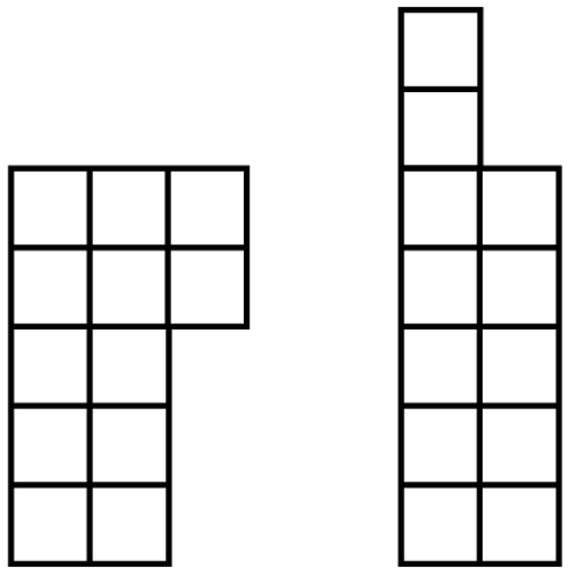
Show a few configurations of 12 tiles that are not rectangles as shown in Figure 2.
- Are these rectangles? Why or why not?
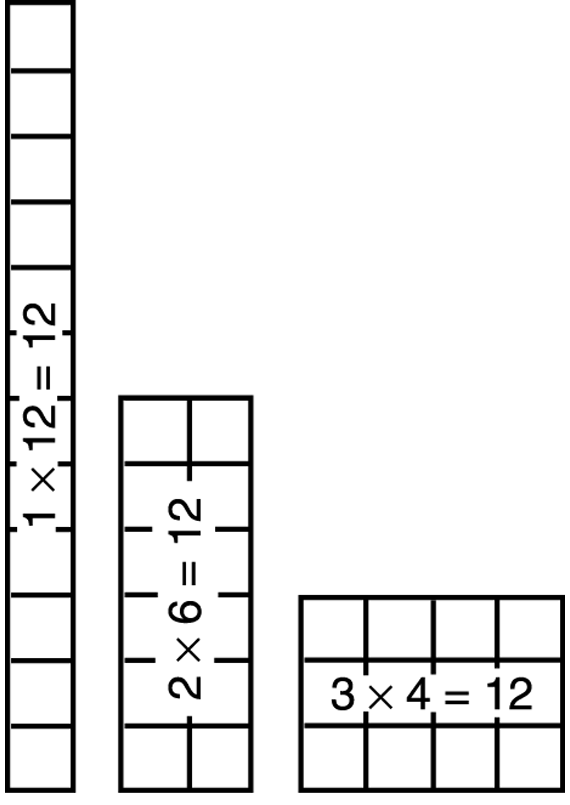
The questions below refer to an array of two rows, 6 tiles in each row, as shown in the picture and table in the Student Guide. Adapt your discussion to the rectangle the class has chosen to discuss.
- How many rows are in this rectangle? (2 rows)
- How many tiles are in each row? (6 in each row)
- What is a number sentence to describe how many tiles are in this rectangle? (2 × 6 = 12)
- What is the area of this rectangle? (12 square inches)
- What is the perimeter? (16 inches)
Turn the set of tiles so that it shows 6 rows of 2 tiles, and ask students to do the same.
- How many rows are in this rectangle? (6 rows)
- How many tiles are in each row? (2 tiles in each row)
- What is a number sentence to describe how many tiles are in this rectangle? (6 × 2 = 12)
- Is the area the same? The perimeter? (Yes, the area is still 12 square inches, and the perimeter is still 16 inches.)
- Did anything change about this array when you turned it? (Only the way we counted rows. Everything else stayed the same.)

Commutative Property of Multiplication. The commutative property of multiplication says that the order of factors in a multiplication sentence does not matter. Both 3 × 4 and 4 × 3 equal 12. In third grade, students used the term turn-around rule instead of commutative property. Either term is appropriate here.
In order for students to appreciate the commutative property of multiplication, ask them to consider whether other operations are commutative. Addition is commutative (4 + 2 = 6 and 2 + 4 = 6). Division is not commutative: six cookies divided among three children gives two cookies per child (6 ÷ 3 = 2 cookies), but three cookies divided among six children gives only one-half cookie per child (3 ÷ 6 = 1/2 cookie). Subtraction is not commutative (5 − 2 = 3, but 2 − 5 = −3).
The commutative property has to do with the order in which things can happen. Putting on your shirt and jeans is commutative (the order in which you do it does not matter), but putting on your shoes and socks is not (the order certainly does matter).
Students might wonder why the commutative property has its name. It might help them to think of the meaning of the word “commute.” Their parents might commute, or travel, to work. The commutative property of multiplication says that the factors in a multiplication sentence can travel, or change places, but their product stays the same.
Explore Turn-Around Facts. Write this number sentence (or the one that matches the array in the class discussion) for students to see: 2 × 6 = 6 × 2.
- Is this a true statement: 2 × 6 = 6 × 2? How do you know? (Yes, because both sides of the equal sign are 12.)
- What does the equal sign tell us in this sentence? (It tells us that 2 × 6 equals the same number as 6 × 2.)
- Does the equal sign always tell us that? (Yes, it always means that two quantities are the same.)
- What is different about the expressions on both sides of the equal sign in the sentence 2 × 6 = 6 × 2? (The order of the numbers is different.)
Discuss with students that the sentence shows that the order of the numbers being multiplied does not matter. Tell students that this is called the commutative property of multiplication, sometimes called the turn-around rule. See the Content Note.
For this activity, have the class agree that the 2 × 6 rectangle and the 6 × 2 rectangle will be considered the same rectangle.
- What other rectangles can be constructed with 12 tiles? (There are two other possible rectangles: 1 × 12 and 3 × 4.)
- Does the commutative property or turn-around rule work for these two rectangles? Is 1 × 12 the same as 12 × 1? Why do you say so? (Yes, because they both equal 12.)
Draw Rectangles with 12 Tiles. After discussing the different rectangles that can be made with an area of 12 square inches, ask students to draw and cut out all three rectangles from the Square-Inch Grid Paper Master you have copied and distributed (Question 2). Have tape available so they can tape pieces together to make long, skinny rectangles. Students should also record an appropriate multiplication sentence on each rectangle, as shown in Figure 1.
Tape an example of each of the three rectangles to a sheet of construction paper and post it.
Make Rectangles with 18 Tiles. Question 3 asks students to investigate the rectangles that can be made using 18 tiles. They should make all the possible rectangles (there are three: 1 × 18, 2 × 9, 3 × 6), draw and cut out the rectangles from Square-Inch Grid Paper, and write appropriate number sentences. Discuss their results. Ask how they can be sure they found all the possible rectangles. Suggest systematically checking each possibility. See the Sample Dialog. Post an example of each of the rectangles for 18 tiles, as you did for 12 tiles.

Teacher: How can you tell that you have all the rectangles?
Tanya: I see a pattern. You could just keep going.
Teacher: What pattern do you see, Tanya?
Tanya: Well, it's 1, 2, 3 rows for the rectangles. The first is 1 times 18, the next is 2 times 9, and then there is 3 times 6.
Jacob: Yes—it was the same for the other one, with the 12 tiles.
Teacher: What were those rectangles, Jacob?
Jacob: 1 × 12, 2 × 6, and 3 × 4.
Teacher: Great. How do you think we can use that pattern to find out if we have all the rectangles?
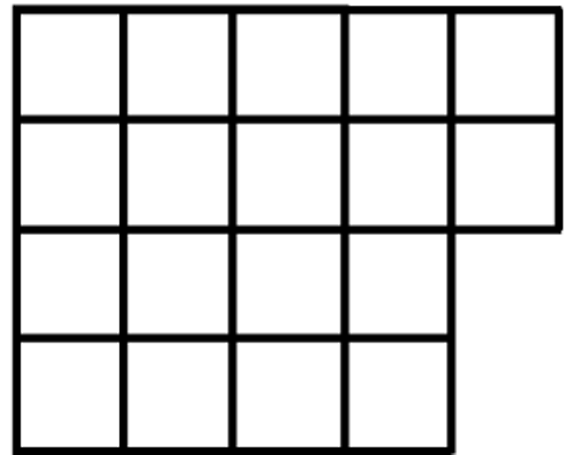
Tanya: We could keep going. We tried 4 rows but it didn't work. When you do it by 4s, you have 2 tiles missing from the last column.
Teacher: Can you show me this with 18 tiles?
[Tanya shows 4 rows of tiles: 2 rows with 5 tiles each and 2 rows with 4 tiles. See Figure 3.]
Teacher: So what does that tell you about 4 and 18, Tanya?
Tanya: There isn't a rectangle with 4 rows. So you can't say 4 times something is 18.
Teacher: What will you do next using your pattern, Tanya?
Tanya: I could try 5 rows.
Teacher: Did anyone try to make a rectangle with 5 rows?
Grace: I did, but it didn't work. Fives go 5, 10, 15, 20. There isn't an 18. It's like with 4. There were 2 missing.
Teacher: How about 6 rows?
Jacob: We already have 6. It's the same as the 3 x 6 rectangle.
Teacher: Can you give the number sentences?
Jacob: 6 × 3 = 18 and 3 × 6 = 18.