Lesson 3

Factors

Est. Class Sessions: 2–3

Developing the Lesson

Part 2. Finding More Factors

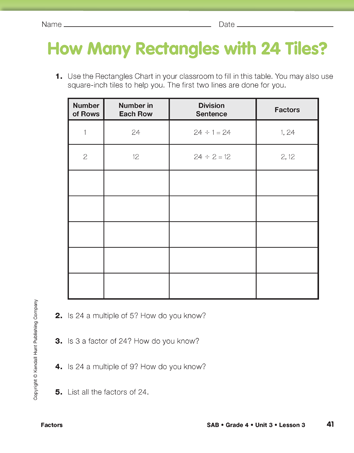
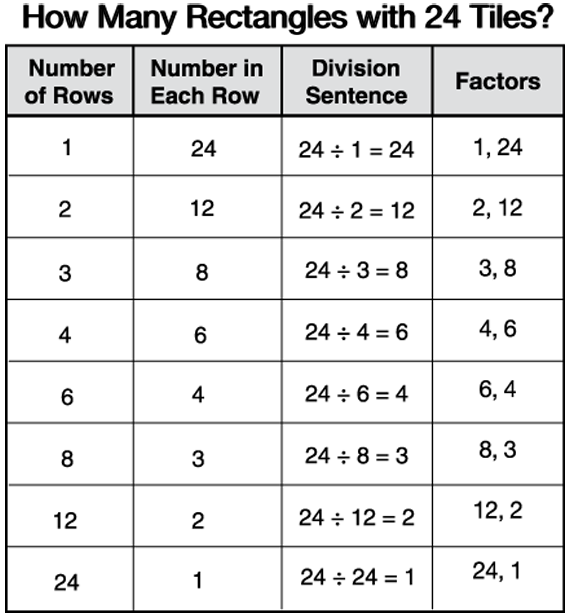
Find the Factors of 24 Using Rectangles. Direct students to the How Many Rectangles with 24 Tiles? page in their Student Activity Book. Ask students to fill in the table. As they work, students can use their calculators or they can refer to the rectangles class chart they made in Lesson 1. In this table, students write division sentences instead of multiplication sentences and they name the factors as they find them. A completed table is shown in Figure 1.

Using division to look for factors is helpful, particularly when using calculators.

X

An easy method of finding all the factors of a number is to make an ordered list of whole number factor pairs. List 1 as a factor with its factor pair, then try 2, then 3, and so on, as shown in the list below of factor pairs of 36. Eliminate 5 as a factor because 36 ÷ 5 does not result in a whole number. As the list continues, the numbers on the left increase and the numbers on the right decrease.

1 × 36
2 × 18
3 × 12
4 × 9
5 × 7.2
6 × 6

Once a number on the right is the same as one on the left, all the whole number factors have been listed. They can be read in order by reading in a U starting at the upper left and finishing at the upper right. 1, 2, 3, 4, 6, 9, 12, 18, 36.

Now consider the factors of 24, using the same system. 1, 2, 3, and 4 are factors because each can be multiplied by another whole number to produce a product of 24.

1 × 24
2 × 12
3 × 8
4 × 6

The next number to be tested is 5, but that does not have a whole number partner. The next number is 6, but that factor has already been listed in the 4 × 6 sentence. Therefore, all the factors of 24 have now been identified, reading in order from the upper left: 1, 2, 3, 4, 6, 8, 12, 24.

From their charts, students can find that the factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24. Note: It is not necessary to list rows with 6, 8, 12, and 24 tiles, as in the table. Some students might prefer to make this complete list. Remind them, however, that the rectangles showing turn-around facts (e.g., 3 rows with 8 in the row and 8 rows with 3 in the row) are considered the same rectangle.

X

Two types of division sentences are possible here. If the total number of tiles is known, and the number of rows is given, then the number in each row can be found. The first type is represented by the division sentences shown in the table (24 ÷ number of rows = number in each row). If students write division sentences representing the second type (24 ÷ number in each row = number of rows), they would also be correct.

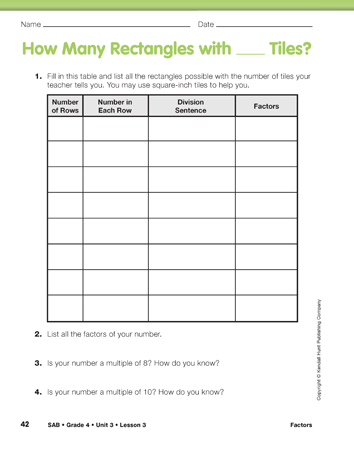
After discussing the factors of 24, ask student pairs to complete Questions 2–5 on the How Many Rectangles with 24 Tiles? page in the Student Activity Book. The next Student Activity Book page, How Many Rectangles with _____ Tiles?, allows you to tailor the activity to the needs of your students based on their success with How Many Rectangles with 24 Tiles? You can ask struggling students to find the factors for 18 or 30. Students who are ready for more of a challenge can find the factors of 36, 56, 72, or some other number that has numerous factors. As students are finding the factors of a number, they are also getting practice with their multiplication and division facts.

Questions 7–15 in the More Finding Factors Problems section of the Homework section in the Student Guide can be assigned at this time.

Student Guide:
Student Activity Book: 41 42
Answers
X
SAB_Mini
+
X
SAB_Mini
+
Master:
Rectangles that can be made with 24 tiles
X
+