Each student has been provided with two extra strips. These can be used if a student loses a strip or makes an error folding.
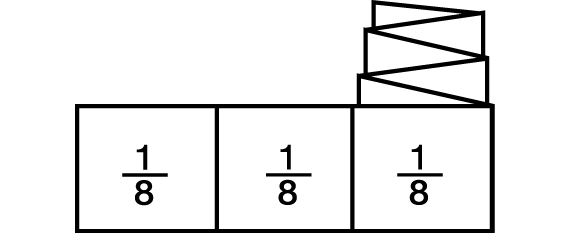
Show Fractions Less Than One. In this activity, students use their fraction strips to represent different fractions. They will need all their completed strips and the strip representing one whole. To start this activity, name a fraction that can be represented using the fraction strips. For example, ask students to show 3/8. To show 3/8, students should use the strip that is divided into eight equal pieces. They fold 5/8 of the strip back and leave 3/8 of the strip showing as in Figure 7.
- What is the denominator in the fraction? What does it tell you? (The 8 is the denominator because the whole is divided into 8 equal parts.)
- What is the numerator in this fraction? What does it tell you? (The numerator is 3 and tells you how many parts are showing.)

Everyday Language, Mathematical Language, and Fractions Greater than One. The terms used in this lesson have different meanings when used in everyday language than in mathematics. When we say, “John ate only a fraction of the cookie,” the term fraction implies that he ate less than a whole cookie. In mathematics, fractions are numbers that can be written in the form a/b (a and b have to be whole numbers). That means that 3/4 and 2/5 are fractions, but so are 9/4 and 7/5, which are numbers greater than one. The term improper fraction is used to refer to fractions such as 9/4 and 7/5 where the numerator is greater than or equal to the denominator. However, there is nothing mathematically improper about them. They are often the most efficient way to write fractions, especially when computing or writing algebraic expressions. Writing fractions greater than one as mixed numbers, such as 23/4 or 12/5, is useful in other situations, especially everyday situations such as in recipes, sewing, and construction projects.
Continue the activity by asking volunteers to choose a fraction smaller than one whole and ask the class to show the fractions with their pieces. Examples include:
Match Fractions with Number Sentences. Explain that you are going to write some number sentences on the board that show repeated addition. Students will use their strips to show the fraction that the number sentence represents.
Write the following number sentences on the board and say:
- Show me 1/4 + 1/4 + 1/4. (Students show 3/4.)
- Show me 1/8 + 1/8 + 1/8 + 1/8 + 1/8. (Students show 5/8.)
- Show me 1/2 + 1/2. (Students show 2/2 or 1 whole.)
Show Fractions Larger Than One. Complete the same activity, but ask partners to show fractions larger than 1 using mixed numbers and improper fractions. Partners will need to work with two sets of strips.
- How can you show 11/2 with your strips? What strips will you need? (Obvious choices are to show the whole red strip and half the pink strip or show one whole pink strip and half a pink strip.)
Tell students 11/2 is a mixed number—a fraction shown using a mix of whole numbers and fractions.
Show students a whole pink strip and half a pink strip.
- How many halves are shown? (3 halves)
Count the halves represented in a whole pink strip and half a pink strip (3). Write 3/2 on the board. Tell students this representation is called an improper fraction: a fraction shown using only a numerator and a denominator when the numerator is equal to or greater than the denominator. See the Content Note for more about mixed numbers and improper fractions.
- What is the denominator? Why? (2; The wholes are divided into two equal parts.)
- What is the numerator? Why? (3; 3 pieces are showing.)
Continue the activity by asking volunteers to name numbers between 1 and 2 for the class to show with their strips. Examples include:
Match Larger Fractions with Number Sentences. Students will continue to work with a partner and two sets of strips.
Write number sentences on the board that use repeated addition to show fractions larger than one and say:
- Show me 1/4 + 1/4 + 1/4 + 1/4 + 1/4 + 1/4. (Students show 6/4.)
- How do you know that this fraction is greater than 1? (We have to use 2 strips to show it.)
- Use a mixed number to name this fraction. (12/4)
- Show me 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8. (Students show 9/8.)
- Is this an improper fraction? How do you know? (It is an improper fraction because the numerator is greater than the denominator, and we have to use 2 strips to show it—one whole and another 1/8 of the eighths strip.)
- Is there another name for this improper fraction? (Yes, 11/8.)
- Show me 1/4 + 1/4 + 1/4 + 1/4. (Students show 4/4 or 1 whole.)
- Is this an improper fraction? How do you know? (It is an improper fraction because the numerator, 4, is not greater than the denominator, but it is equal to it.)
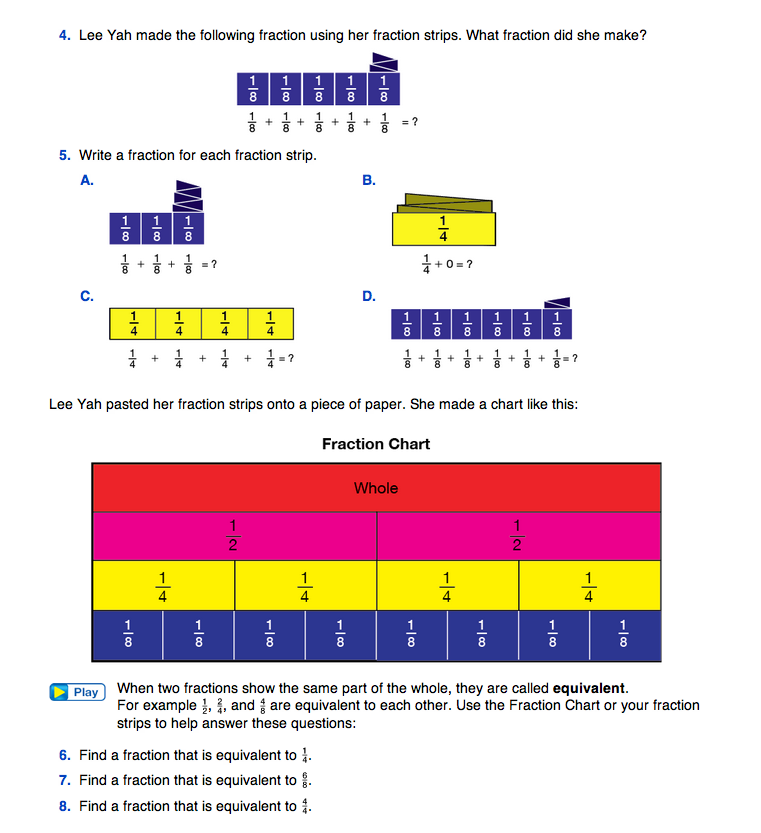
Use Questions 1–3 on the Fraction Strips pages in the Student Guide to review what a fraction is, the definition of the denominator, and the definition of the numerator.
- Line up your fraction strips with one whole at the top and the others in the order that you made them: halves, fourths, eighths. Which fraction strip—halves, fourths, or eighths—has the smallest number in the denominator? (The halves have a 2 in the denominator.)
- Which fraction strip has the largest number in the denominator? (eighths)
- Show 1/2, 1/4, and 1/8 with your strips. Which is the largest fractional part of the whole? Which is the smallest fractional part of the whole? (1/2 is largest and 1/8 is smallest.)
- What happens to the size of the equal parts on the strips as the denominator gets larger? (The fractional parts get smaller.)
- Why? (The denominator tells you how many parts to divide the strip into. The more parts you divide the strip into, the smaller the part.)
Questions 4 and 5 provide practice naming fractions that are represented with fraction strips. Direct students' attention to the number sentences accompanying each strip.