Lesson 9

Comparing Fractions Using 12

Est. Class Sessions: 2

Developing the Lesson

Part 1. Comparing Fractions Using 12

Use Denominators to Order Fractions. Launch this lesson by introducing the pizza problem in Question 1 of the Comparing Fractions Using 12 pages in the Student Guide. Student pairs use their fraction circle pieces to answer and discuss Questions 1B–E. Ask a few students to share their strategies for Question 1D.

Ask:

What is the unit whole in the problem? (a whole pizza)
Who ate more pizza, each student at Table A or Table B? (Each student at Table A. Possible explanations: The orange pieces are larger than the yellow. Students at Table A have to share with fewer people than Table B.)
What do you notice about the numerators in this problem? (They are both 1.)
What do you notice about the denominators in this problem? (They are different.)
What do the denominators tell about which fraction is larger? (The larger the denominator, the smaller the piece of pizza, because the whole is shared with more people.)
Name a fraction smaller than 14.
(Possible responses: 18 or 112)

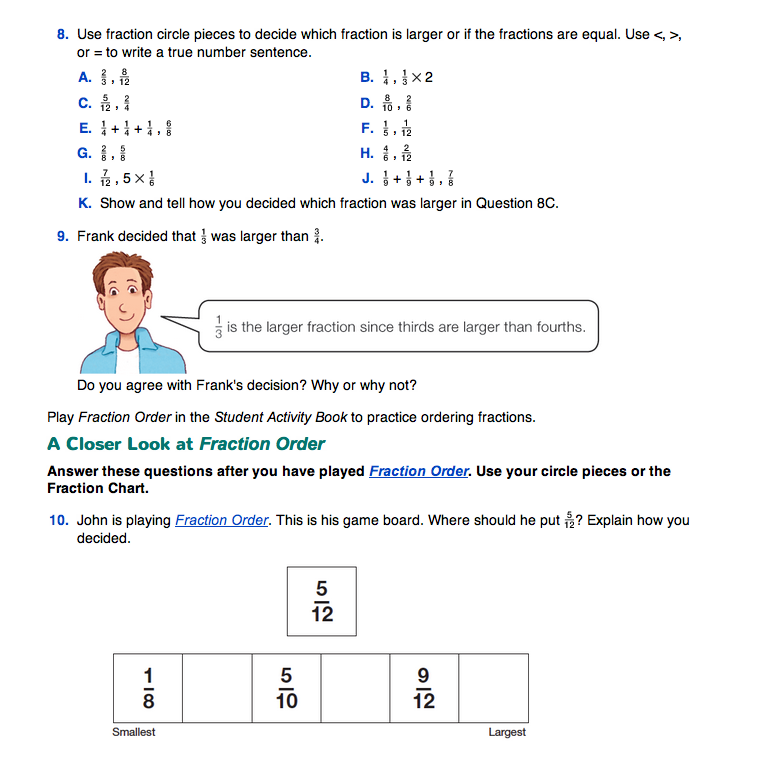
Continue this discussion with Question 2. Like the pizza problem, students are comparing the eaten portion of each pie. Give student pairs a few minutes to answer Questions 2A–F. While they are working, choose a few students to create a fraction card on an index card for each of the fractions (212, 26, and 24) in this problem. See Figure 2 for an example. After pairs have had a chance to solve the problems, ask a few students to share their strategies for Questions 2E and 2F.

Ask:

What is the unit whole in this problem? (A whole pie)
Who ate more pie? (Brandon ate the most. Possible explanation: Two yellow pieces are larger than two black pieces. His pie was divided into fewer pieces, so each is larger.)
What do you notice about the numerators in this problem? (They are all 2.)
What do you notice about the denominators in this problem? (They are different.)
What do the denominators tell about which fraction is larger? (The larger the denominator, the smaller each piece of pie.)
Explain why that is true. (The denominator tells how many equal pieces are in the pie. A larger denominator means the pie will be divided into more pieces. More pieces means smaller pieces.)
Put the fractions 26, 24, and 212 in order from smallest to largest. (212, 26, 24)
How did you decide the order for these fractions? (Possible response: I looked at the numerators and they were all the same, so I knew I could use the denominators to put them in order. I know that the bigger the denominator the smaller the fraction because it means that the whole is divided into more pieces, so each piece would be smaller. I knew 212 was the smallest, 26 was next, and 24 was the largest.)

Students need many experiences with concrete materials such as circle pieces and fraction strips to develop mental images of fractions, so they can develop number sense for fractions. Visually comparing to benchmarks like 12 is a powerful strategy for determining relative sizes of fractions.

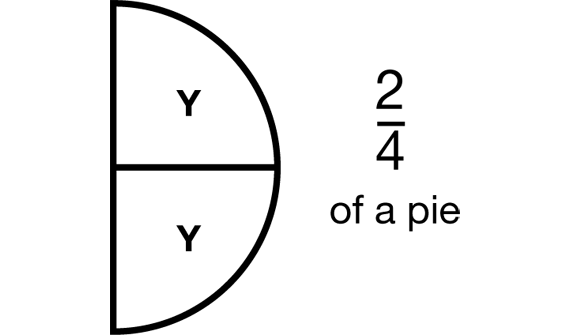
Use a Benchmark Number Line. Show students the number line you created (Figure 1 or 3) and point out how the fraction circle pieces relate to the pictures above the number line.

Help students make the connection between the area model of a fraction and the number line representation.

Ask:

What fraction circle piece is the unit whole on this number line? (the red circle)
Where is the red circle placed? (above number 1)
Why is the red circle placed at “1”? (Because 1 is the whole distance we are looking at.)
What is the unit whole on this number line? (The entire distance between 0 and 1.)

Using the fraction cards the students created for Question 2, discuss where these fractions are on the number line.

Ask:

24 of the peach pie is eaten. Where does this fraction go on the number line? How do you know? (At the 12 benchmark. Possible explanation: 24 is equal to 12 because I can cover the 2 yellow pieces with 1 pink piece; 2 is half of 4, so I know that 24 is equal to 12.
Which fraction is larger, 212 or 26? How do you know? (26 is larger because both numerators are 2, and sixths are larger than twelfths.)
Is 26 larger or smaller than 12? How do you know? (26 is smaller than 12. Possible explanation: because I cannot cover a pink piece with 26.)
Is26 closer to 12 or to zero? How do you know? (Closer to 12 , because most of the pink piece is covered.)
Where does 26 go on the Benchmark Number Line? [Place the appropriate fraction card between zero and 12 but closer to 12.]
[Refer to the 212 fraction card.] Is 212 larger or smaller than 12? How do you know? (212 is smaller than 12. Possible explanation: 612 would be equal to a half because 6 is half of 12 and 212 is less than 612.)
Is 212 closer to 12 or to zero? How do you know? (Closer to zero, because I know 612 equal 12 and the numerator 2 is closer to zero than to 6.)
Where does 212 go on the Benchmark Number Line? [Place the appropriate fraction card between 0 and 12 but closer to zero.]

Fractions Between 12 and 1. Question 3 asks students to find two fractions greater than 12 using fraction circle pieces. Ask students to work on this problem in small groups. Students tell the members of their group how they know their fractions are larger than 12 . While students are working, choose a few students and give them an index card to create more fraction cards to place on the class number line. After groups have discussed Question 3, collect some sample responses from the class. Have the students model and record their responses and place fraction cards in the appropriate places on the Benchmark Number Line.

Ask:

How do you know this fraction is larger than 12? (Possible response: I can see that one pink (12) covers some of the fraction, but there is some not covered.)
How do you know if this fraction is closer to 12 or closer to 1 whole? (Possible response: I look at the size of the piece not covered by 12 . If the leftover part is close to the size of the pink piece, then the fraction is close to 1 whole.)
Where should this fraction go on the Benchmark Number Line?

Place the student-created fraction cards on the display of the Benchmark Number Line between 12 and one. Some will be placed closer to a whole and others closer to 12. Stack fraction cards with equivalent fractions. Some fractions may be too close to each other for students to determine the exact order.

Fractions between 0 and 12. Question 4 asks students to find two fractions smaller than 12 using fraction circle pieces. Students should explore this question in small groups as they did for Question 3. While students are working, choose a few students and give them an index card to create a fraction card to place on the display of the Benchmark Number Line.

Ask:

How do you know this fraction is smaller than 12? (Possible response: The fraction covers part of a pink piece, but not all.)
How do you know if this fraction is closer to 12 or closer to 0? (Possible response: If the fraction covers most of the pink piece, then the fraction is closer to 12. If it covers very little of the pink piece, then the fraction is closer to zero.)
Where should this fraction go on the Benchmark Number Line?

Place the student-created fraction cards on the Benchmark Number Line between zero and 12. Place some closer to zero and others closer to 12 . Stack fraction cards with equivalent fractions. Some fractions may be too close to each other for students to determine the exact order.

Assign Questions 5–7 on the Comparing Fractions Using 12 pages in the Student Guide. The Sample Dialog Box 1 has three examples of possible strategies for Question 5.

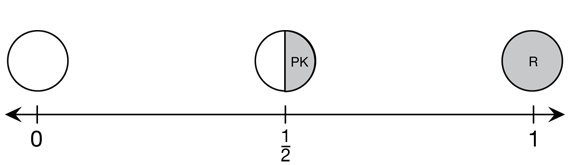
Below are student responses to Question 5: Is 25 greater than, less than, or equal to 12? Use these as models to better understand what your students are thinking.

Alex

Alex: I think 25 is less than 12 because I looked for 12 (pink piece) and the fraction is smaller than 12.

Teacher: Is 25 closer to 12 or closer to zero?

Alex: 25 is closer to 12 because the fraction covers most of the 12 (pink) piece. [Alex drew the picture below.]

Lily

Lily: I think 25 is greater than 12 because 12 is a larger fraction than 15.

Teacher: Does the problem ask you to compare 15 or 25?

Lily: 25.

Teacher: Is 15 equal to 25?

Lily: No, this is 25. [She uses the green circle pieces.]

Teacher: Is 25 greater than or less than 12?

Lily: [Pause] I looked at the bottom number [denominator] and forgot that I have to look at the top number, too. When I look at the fraction pieces I can see that 25 is a little less than 12.

Teacher: Is 25 closer to 12 or zero?

Lily: 12 because 25 is only a little bit less than 12.

Julie

Julie: I think 25 is less than 12 but I did not use the circle pieces.

Teacher: What did you do?

Julie: I know that 2 12 is half of 5. So 2 is less than half of 5 and 3 is more than half of 5. So 25 is less than 12 and 35 is bigger than 12.

Teacher: That is an interesting strategy. Do you think that would work all the time? Try a different problem.

Julie: Okay, 512 is less than 12 because 612 is equal to 12 and 512 is less than 612.

In Question 6, students will use the fraction circle pieces to solve some repeated addition and multiplication number sentences before determining if the fractions represented are greater than, less than, or equal to 12.

As students are solving Question 7, choose a few students to create a fraction card to place on the Benchmark Number Line. Review Questions 7A–C with the class using the student-created fraction cards and the Benchmark Number Line.

Assign Questions 8 and 9. Remind students of how to use the symbols <, >, and =. Question 9 presents a common misconception a student might have when comparing fractions. Ask students to discuss what they would tell Frank about his comparison.

Students are not expected to master comparing fractions using numerical relationships in symbols in fourth grade. Students need experiences with concrete models to develop a quantitative notion of fractions. Students should be allowed and encouraged to use models at this level.

Questions 1–3 of the Homework Section in the Student Guide can be assigned after Part 1.

Student Guide: 342 343 344

Answers