Lesson 10

Multiplying Fractions by a Whole

Est. Class Sessions: 2–3

Summarizing the Lesson

Display the charts of strategies students created during Part 1 and the chart paper titled “Ming's Strategy” you created. (See Materials Preparation.) Refer students to Question 16 in the Student Guide. Ask students to solve 3/4 × 12 using any tool or strategy with which they feel comfortable. Ask a student to record a solution using each of the strategies represented on the chart paper (e.g., Irma's Strategy).

Ask:

X
  • Is Linda's strategy similar to Irma's, Roberto's, Shannon's, or Jacob's strategy? (Roberto's)
  • Is Ming's strategy similar to Irma's, Roberto's, Shannon's, or Jacob's strategy? (Possible responses: Shannon's because Shannon thought of a set of circles. Or not similar to any of them. He used a set of things rather than an area model.)

Then ask them to compare Linda's strategy to Ming's strategy. Students should notice that, in general, Ming's strategy is more efficient than Linda's repeated addition strategy. Ask student pairs to solve the problems in Question 17 using Ming's strategy.

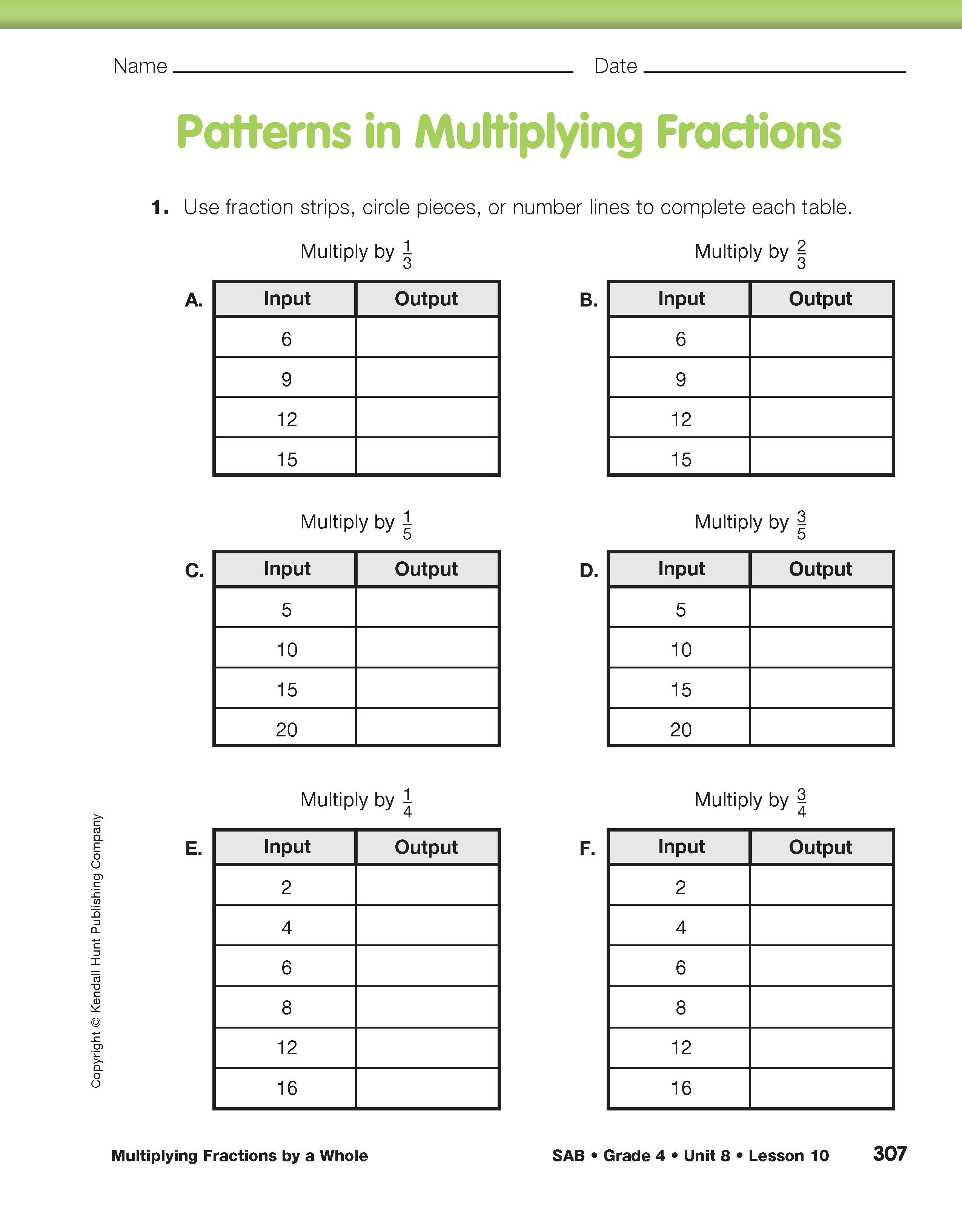
For additional practice, assign the Patterns in Multiplying Fractions pages in the Student Activity Book.

Distribute and assign the Multiply Fractions Assessment Master.

X

Use the Multiply Fractions Assessment Master with Feedback Box to assess students' abilities to multiply fractions by a whole number [E11] using models and number lines [E1].

Student Guide:
Student Activity Book: 307 308
Answers
X
SG_Mini
+
X
SG_Mini
+
Master: