Direct students' attention to the vignette after Question 11 in their Student Guide. Mrs. Dewey asks what fraction of an orange Daniel ate if he ate 5 of 6 orange halves. This highlights the connection between repeated addition and multiplication of a fraction by a whole number.
Read the vignette and then ask:
- What is the unit whole in this situation? (one orange)
- The unit whole is one orange, and the whole oranges are cut into halves. How many halves does Daniel eat? (5 halves)
- Is that more than a whole orange? (Yes)
- What fraction would you write to show how much of an orange Daniel ate? (5/2)
- Explain how this fraction shows that Daniel ate more than a whole orange. (It is an improper fraction. 2/2 is a whole, but he ate 5/2. So he ate more than a whole orange.)
- Explain Luis's way of thinking. (Luis added one-half 5 times. He counted the halves on his fraction strips and got 5 halves.)
- Explain Shannon's way of thinking. (Instead of repeatedly adding 1/2 to 1/2, Shannon multiplied 5 times 1/2 to get 5/2 or 21/2.)
- How are they different? (Luis uses repeated addition and Shannon uses multiplication.)
- How are they the same? (They both put 5 halves together to come up with 5/2 or 21/2.)
- Is 1/2 + 1/2 + 1/2 + 1/2 + 1/2 = 5 × 1/2 a true number sentence? Why or why not? (It is a true number sentence because both sides of the equation show the same amount.)
- Imagine that Grace said because Daniel ate 5 of the 6 orange halves, he ate 5/6 of an orange. Is that correct? Explain. (No. The unit whole is one orange, not the amount of halves in the bowl. Also, I know that he ate more than a whole orange. 5/6 is less than a whole.)
- How could we change the question so that the answer would be 5/6? (We could ask, “How much of the orange halves in the bowl did Daniel eat?” He ate 5/6 of the orange halves in the bowl.)

In the vignette about Daniel's orange halves, students may have confusion regarding the unit whole. In this vignette, the unit whole is one orange. It is not the bowl of 6 orange halves. The question asks what fraction of an orange did Daniel eat. He eats 5 of the (6) halves, so he eats 5/2 of an orange—more than a whole orange. Students may incorrectly think that he ate 5/6 of an orange. If the question were reworded to read, “What fraction of the orange slices in the bowl did Daniel eat?” then 5/6 would describe that amount.
Display the class list of number sentences where students can see it, so students can refer to it throughout the unit.
At this point in their study of fractions, students may solve some problems using repeated addition (e.g., 1/3 + 1/3 + 1/3 + 1/3 = 4/3) or by multiplying fractions by a whole number (e.g., 1/3 + 4 = 4/3). Either way is acceptable. Further, sums or products may be expressed as improper fractions (4/3) or as mixed numbers (11/3). Either is acceptable.
Assign Questions 12–19. Students work together with partners and two sets of fraction strips to solve word problems. Problems may be solved using repeated addition (e.g., 1/2 + 1/2 + 1/2 = 3/2) or by multiplying fractions by a whole number (e.g., 1/2 + 3 = 3/2). Either way is acceptable.
After students have completed the problems, ask them to share their solutions. As volunteers discuss the solutions, write some of the number sentences on the board. It is important to recognize that students may write addition sentences such as
1/3 + 1/3 + 1/3 + 1/3 = 4/3 or 11/3 or multiplication sentences, 4 + 1/3 = 4/3 or 11/3. Sums or products may be expressed as improper fractions or as mixed numbers. Either is acceptable.
To discuss Question 12 ask:
- For Question 12, what number sentence did you write to show how many jars of shells the girls had? (11/4 + 2/4 = 13/4)
- How does your number sentence match the problem? Show me with your strips. (Students will use 2 yellow strips to show 1 whole plus another 1/4 represents Irma's jars of shells, and 2/4 more on that strip represents her sister's jar of shells. Together they have 13/4 jars full of shells.)
- How did you decide how much more they needed to fill two jars? (Possible answer: I looked at the 2 yellow fourths strips and saw that they had 13/4 jars already. I knew if I added 1/4 more, that would be 2 wholes, or 2 jars full.)
To discuss Question 13 ask:
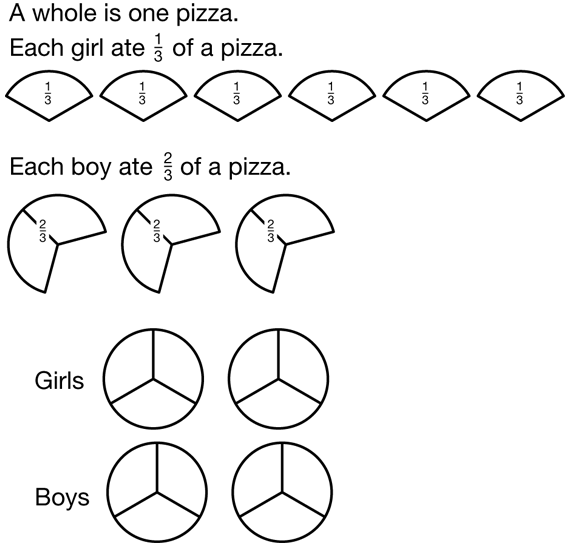
- In Question 13, who ate more pizza at the party—the boys or the girls? (They both ate the same amount.)
- Explain how you solved the pizza problem. (Possible response: See Figure 2. I drew a picture of some pizzas. I cut each pizza into 3 equal parts. Since six girls each ate 1/3 of a pizza, I drew six 1/3 parts. Then, since three boys each ate 2/3 of a pizza, I drew three 2/3 parts. I noticed that I had the same number of parts for each group. All together, the girls ate 2 whole pizzas and the boys ate 2 whole pizzas, too.)
- Can you write a number sentence for this problem? (Answers will vary. 1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 = 2/3 + 2/3 + 2/3, 1/3 + 6 = 2/3 + 3, 6/3 = 6/3, or 2 = 2.)
- Is 6 × 1/3 = 3 × 2/3 a true number sentence? Show us with your fraction strips. (Yes. Students show that six 1/3 parts are equivalent to three 2/3 parts on their strips.)
- Does this solution make sense? (Yes. The group of 6 girls each eats 1/3 of a pizza. The group of 3 boys has half as many kids, but they each eat twice as much pizza, 2/3. That makes the amount of pizza they eat equal.)
- Did anyone solve this problem another way? (Possible response: I knew that I was going to add 1/3 six times, so I just multiplied 6 × 1/3 and got 6/3. Then, I added 2/3 + 2/3 + 2/3 with my fraction strips and got 6/3 again. I knew each group ate the same amount of pizza.)
To discuss Question 15 ask:
- Is 7/6 + 3/6 = 10/12 a true number sentence? How do you know? (Possible response: No, because both sides of the equal sign do not show the same amount. 7/6 + 3/6 = 10/6, not 10/12. I know that 10/12 is less than 1, but 7/6 is already greater than 1, then I have to add 3/6 more to that, so it will be more than 1. A sum of 10/12 doesn't make sense.)
- Work with a partner to show how to correctly add
7/6 + 3/6 with your strips.
- What did Maya do incorrectly? (She added the denominators, 6 + 6, together like she did the numerators.)
Question 17 asks students to solve number sentences while adding and subtracting fractions with like denominators. Question 18 involves multiplying fractions by a whole number. Check-In: Question 19 asks students to write both addition and multiplication sentences for fraction problems.
Students complete Check-In: Question 19 in the Student Guide to demonstrate their progress toward the following Expectations: naming and representing fractions greater than one using models [E5], writing number sentences from area models of fractions [E6], and multiplying fractions by a whole number [E11].
Play Show Me from Lesson 2 or Fraction Fill from Lesson 7 to provide targeted practice with naming and writing fractions.