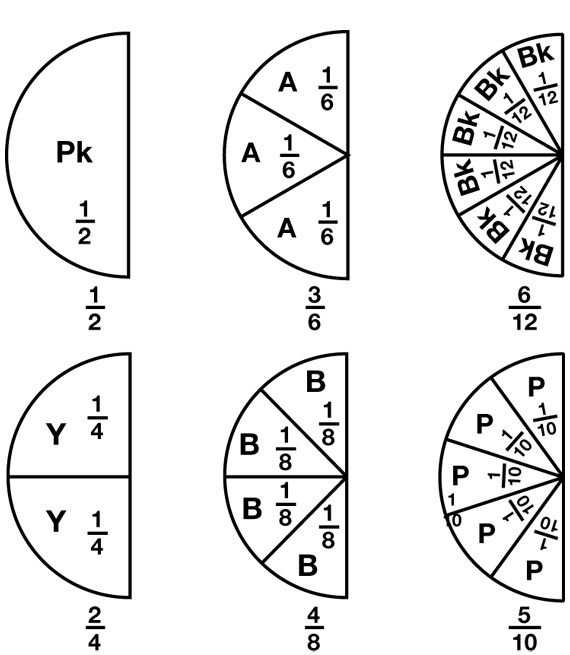
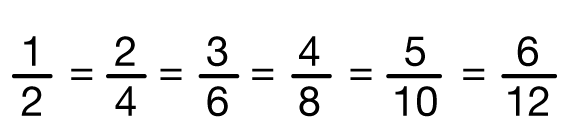Explore Fractions Equivalent to 1/2. Ask students to take out a red circle and to cover the circle with 1 pink.
Referring to the fraction circle pieces, ask:
- What fraction of the red circle is covered with
pink? (1/2)
- Cover the pink piece with 2 pieces of the same color. Name the fraction of the red circle covered by two pieces. (2 yellow pieces; 2/4)
- Cover the pink piece with 3 pieces of the same color. Name the fraction of the red circle covered by the three pieces. (3/6)
- Find other ways to cover the pink piece with all one color. Name the fractions of the red circle. [See Figure 1.]
Collect student responses on chart paper or have volunteers show them using overhead circle pieces. Have students label the fraction pieces and write the fraction represented below each picture. See Figure 1 for possible responses.
- What do you notice about all of these pictures? (The same space is covered, but the space is divided into different-sized pieces.)
List the equivalent fractions on the board as shown in Figure 2. Explain that fractions with the same value are called equivalent fractions.
Equivalent Fractions. In mathematics, two fractions that have the same value are considered equivalent fractions. At this level of mathematics, we do not distinguish between the words equal and equivalent. Therefore, it is acceptable for students to use either equal or equivalent when comparing two fractions that have the same value.
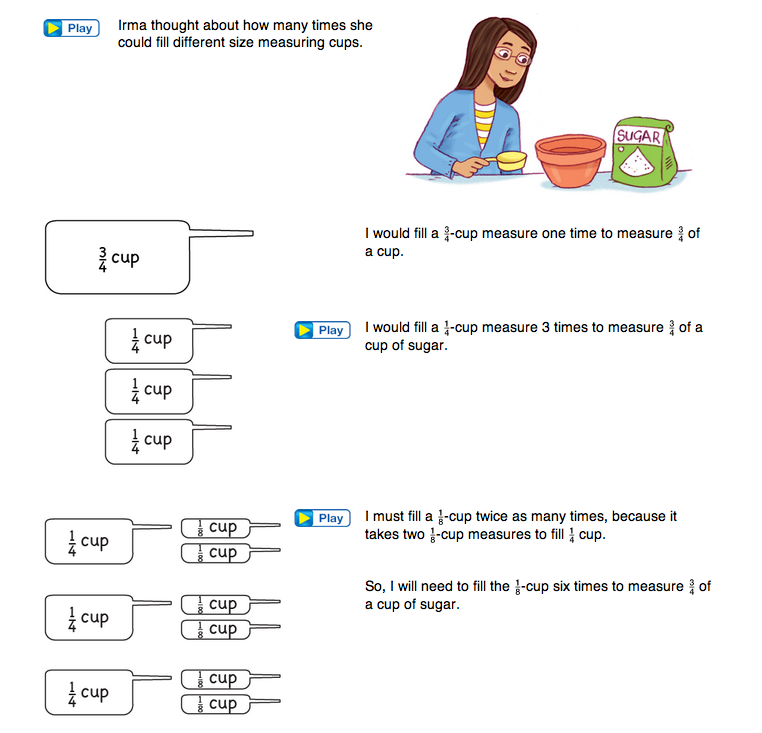
Explore Other Equivalent Fractions. Introduce students to the problem posed in Question 1 of the Equivalent Fractions pages in the Student Guide.
In Question 1, Irma and her friends are making cookies and need to measure 3/4 cups of sugar but have only a 1/8-cup measure. Students can use fraction circle pieces or the Fraction Chart to represent the parts of the problem. After students have had a chance to solve the problem, ask a few students to share their solutions.
- What is the problem asking? (To use the 1/8 measuring cup to measure 3/4 cup of sugar. 3/4 is the same as how many eighths?)
- Show us how you used the fraction circle pieces to solve the problem.
- Show us how you used the Fraction Chart to solve the problem.
- Are there other ways to solve the problem? (Draw a picture.)
Demonstrating the problem in Question 1 with actual measuring cups will help students visualize the problem.
Use Question 2 to explore and compare some solution strategies for this problem.
Some additional questions to deepen the discussion are:
- Which strategy is most like yours?
- Which strategies are similar? (Maya and Ming both used area models to solve the problem. One used the Fraction Chart and the other used circle pieces. Both came to the same answer. Both counted the number of eighths it took to equal 3/4.)
- How is Irma's strategy different? (Irma thought about how many eighths equal one-fourth and used that relationship to find the total number of eighths in 3/4 cup.)
Use Question 3 to summarize the equivalent relationships students explored while solving Irma's measuring cup problem.
Assign Questions 4–7 of the Equivalent Fractions pages in the Student Guide. These problems give students a chance to find and represent equivalent fractions using circle pieces, Fraction Charts, and number sentences.
Review and discuss solutions.
Require students to use area models to show and verify their answers. Research shows students need a chance to see the equivalent relationships with models and representations before the algorithm is presented or required. Students then have a solid understanding of where the numbers come from and have a way to verify their answers.