Multiplying Fractions by a Whole

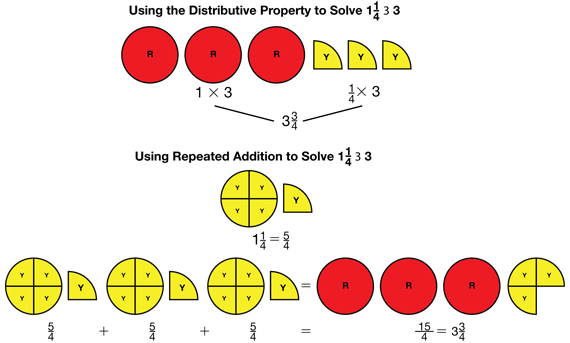
Invent Strategies to Multiply. Refer students to the first Multiplying Fractions by a Whole page in the Student Guide. As you read and introduce the situation in Question 1, be sure students understand the recipe and the problem situation. Keenya needs to change the ingredient amounts to serve more people. Once students understand the situation, ask groups of three or four students to work together to answer Question 1B. Encourage students to combine their circle pieces and strips or to draw pictures to show fractions larger than one whole. Allow students to invent their own strategies and to use the models to explain their thinking.

As you circulate, identify students who will share their strategy with the class. Choose a variety of strategies and models. Ask these students to share their strategies and explanations with the class. Ask students to use some of the strategies they have heard to solve Questions 2 and 3 in the Student Guide.

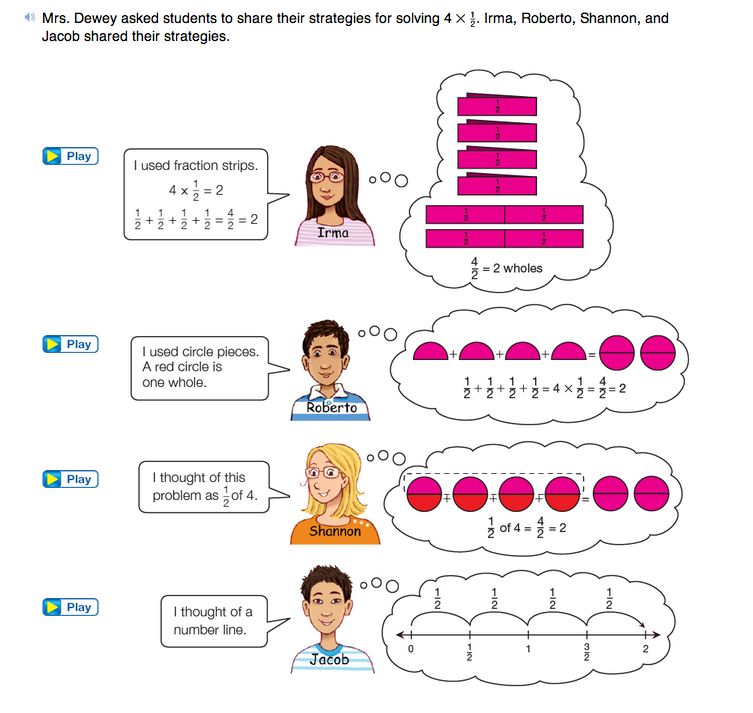
Use Invented Strategies. Display the vignette after Question 3 in the Student Guide. Ask student pairs to read each strategy and to be prepared to explain and demonstrate each strategy to the class.

After pairs have had a chance to explore and use each strategy to solve 3 × 1/4, ask students to record their solutions on the corresponding sheets of chart paper you prepared and have displayed. (See Materials Preparation.)

Assign pairs to work on Question 4 in the Student Guide. Students are asked to use a variety of strategies to solve multiplication problems. As they are working, ask each student to record a solution to one of the problems. Look for a variety of strategies. For example, identify one student who solves 3 × 1/4 with fraction strips and another student who solved the same problem with a number line. Ask students to record their strategy on the corresponding sheet of chart paper. For example, students recording a solution with fraction strips should record their solution on the chart paper identified as “Irma's strategy.”