Ask questions to quickly review ideas in the lesson. Refer to the class list of number sentences for Questions 1–7 as shown in Figure 3.
Choose a question and ask:
- How does the number sentence match the problem? Show me with your strips.
Ask students to discuss the following questions with their partners.
Then discuss them as a class:
- How do you know which strip to use to solve the problem? (I look at the denominators in the fractions in the problem.)
- What do denominators tell you in any fraction? (how many equal pieces the whole is divided into)
- What do the numerators tell you in the fraction sentences? (how many of each piece on the fraction strip to put together [add] or fold back [subtract])
Ask students to work together to solve the following problems and to write a number sentence to match. Tell them that they will need to show or tell how they solved the problems and how they know their answers are correct.
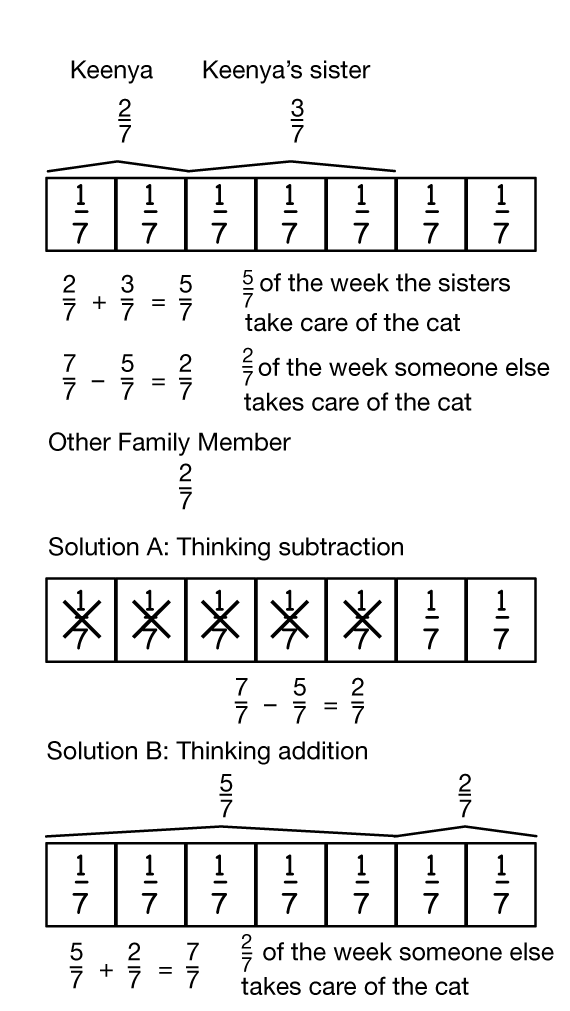
- Keenya and her sister do chores at home. Keenya takes care of the cat 2/7 of the week and her sister takes care of the cat 3/7 of the week. What part of the week do Keenya and her sister take care of the cat altogether? Write a number sentence to match the problem. Look for patterns. (2/7 + 3/7 = 5/7)
- What fraction of the week does someone else in the family take care of the cat? (7/7 − 5/7 = 2/7 of the week)
Because they do not have sevenths strips, students may use a calendar, draw pictures, or use the patterns they see in the class list to solve the problems. A drawing is a good way to show that they know they are correct. Possible solutions and explanations are shown in Figure 4.
Students will likely see the pattern that, when the denominators are the same, they can add or subtract the numerators. It is important that students justify their answers with drawings or a clear explanation so that they know their answers make sense.
- What do you notice about the numerators in this problem? (They are all 1.)
- What do you notice about the denominators in this problem? (They are all the same. They are all 7.)
- When we add or subtract fractions with like denominators, like the sevens in this problem, what do we do? (We just add or subtract the numbers on top, the numerators.)
- What happens to the denominators? (The denominators just stay the same.)
- Does it make sense that the denominators just stay the same? (Yes, because the size of the part doesn't change. Only the number of parts I am adding or taking away does.)
- Keenya’s cat drinks 1/4 cup water daily. How much does he drink in a week? Work with a partner to show me with your fraction strips. (Students use 2 yellow strips to show seven 1/4 parts, folding 1/4 back.)
- Write an addition sentence for this problem.
(1/4 + 1/4 + 1/4 + 1/4 + 1/4 + 1/4 + 1/4 = 7/4)
- Write a multiplication sentence for this problem.
(1/4 × 7 = 7/4)
- Is 1/4 + 1/4 + 1/4 + 1/4 + 1/4 + 1/4 + 1/4 = 1/4 × 7? Explain using your fraction strips. (Yes. Students can show how adding 1/4 to 1/4 seven times is the same as multiplying 7 times 1/4, which is like seven 1/4 parts on their strips.)