Exploring Fractions
WHAT ARE FRACTIONS?

A fraction in everyday language is a part of a whole thing. We think of fractions as numbers … read more
A fraction in everyday language is a part of a whole thing. We think of fractions as numbers that look like 1/2 or 3/5 . Mathematically, a fraction is a number that can be written in the form ( a/b ) with certain conditions. The numerator and denominator must be whole numbers and, since division by zero is problematic, the denominator cannot be zero. Using this definition, 1/2 and 3/5 are clearly fractions. However, it is important to note that 5/5 and 5/4 are also fractions.
There is significant research-based evidence that students develop initial fraction concepts through the use of multiple conceptual representations, including fraction circles, number lines, and drawings. Students make connections among these representations as well as to written symbols. Students use the models to develop concepts about the unit whole, equal parts of the whole, order, and equivalence before developing procedures for translating between symbols or computing with fractions (National Research Council, 2001; Lamon, 2006; Cramer, Post, and delMas, 2002; Cramer and Wyberg, 2012).
Type of Fractions
A fraction can represent any of the following depending on the context … read more
Type of Fractions
A fraction can represent any of the following depending on the context:
- number of parts of a whole
- a point on a number line
- indication of division
- pure number
- ratio, or comparison of one quantity to another
- probability
The first two meanings will be explored in this unit. Fractions that tell the number of parts of a whole are known as part-whole fractions. It is important for students to understand what is meant by the whole for a given part-whole fraction. For example, the whole can be one continuous item (as with 3/4 of a pizza), or a set of separate things (as with 2/3 of all the students in the class). Fractions can also be shown as locations on the number line that lie between whole-number locations. This representation shows the numerical value of fractions relative to other fractions and benchmark numbers (e.g., 0, 1/2, and 1).
Students need to understand that although fractions occur in different situations, the mathematical procedures for naming, comparing, and operating on fractions are the same.
To make connections among the various contexts in which fractions arise, students explore fractions using a broad selection of concrete materials. In this unit, students start with strips of paper that are folded into equal segments. They use a circular area model (circle pieces) to review concepts developed in previous grades and to investigate mixed numbers and improper fractions. Students also use a number line model to compare fractions and to find equivalent fractions.
MULTIPLE REPRESENTATIONS

Children need exposure to a variety of concrete models and mathematical interpretations … read more
Children need exposure to a variety of concrete models and mathematical interpretations of fractions in order to understand the underlying concepts before they can develop meaningful procedures with symbols (Cramer et al., 1997). Therefore, in this unit, students focus primarily on concept development about fractions by using manipulatives and drawings.
Research suggests that although students are able to draw on their informal or “real-life” knowledge of fractions to solve problems, premature attempts at using symbolic procedures can interfere with the construction of meaningful algorithms (Mack, 1990). For example, when students are presented with a problem such as 1/2 + 1/4, their answers are often incorrect because they try to add numerators and denominators based on a whole-number algorithm. The same students are often able to solve the same problem correctly when it is presented in a context, such as:
Ana ate 1/2 of a pizza for dinner and another 1/4 of the pizza for a snack. How much of the whole pizza did she eat?
They use their knowledge of the real world to think through the problem using context and imagery, and then find a solution that makes sense to them.
AREA MODELS

Circle Pieces
Activities in this unit rely heavily on students' use of circle pieces to represent fractions … read more
Circle Pieces
Activities in this unit rely heavily on students' use of circle pieces to represent fractions. Circle pieces provide an area model for part-whole fractions that students can manipulate, visualize, and experiment with as they explore fraction concepts. Research conducted by the Rational Number Project at the University of Minnesota (Cramer and Wyberg, 2012) demonstrates that the circle model is especially useful for students to construct mental images of fractions, compare fractions, and estimate sums and differences. See Figure 1.
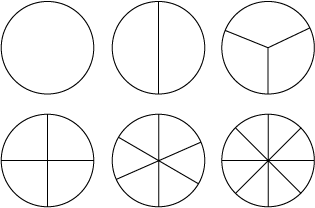
Fraction Chart
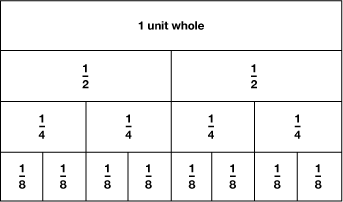
Students build the fraction chart from folded paper strips as shown … read more
Fraction Chart
Students build the fraction chart from folded paper strips as shown in Figure 2. The fraction chart model also supports the development of mental images that help students compare fractions. In particular, it develops students' understanding of the role of the denominator in determining fraction size, i.e., the larger the denominator, the smaller the fractional part (Cramer, Post, and delMas, 2002; Cramer and Wyberg, 2012).
For these reasons, students need sufficient time and opportunity to explore these models. Students should consistently use them to solve problems and develop mental images of fractions in fourth grade as well as in later grades.
NUMBER LINES

Locating fractions on number lines helps reinforce the fact that fractions are numbers … read more
Locating fractions on number lines helps reinforce the fact that fractions are numbers, just as whole numbers are. Number lines give a visual representation of the order of fractional numbers that helps students understand their relative size.
To represent fractions on the number line, divide the interval from zero to one into equal parts. Then label each mark to show what fraction of the distance from 0 to 1 it is. Figure 3 shows fifths on the number line. The interval from 0 to 1 is divided into five equal parts. The length of each part is one fifth of the distance from 0 to 1. The label 1/5 is at the place that is 1/5 of the distance from 0 to 1, 2/5 is at the place that is 2/5 of the distance from 0 to 1, and so on.

CONCEPTUAL CHALLENGES in FRACTION LEARNING

When students begin to study fractions, they usually have a good understanding of the system … read more
When students begin to study fractions, they usually have a good understanding of the system of whole numbers. Unless students develop a conceptual understanding of fractions, this understanding of whole number concepts can interfere with their abilities to work with fractions. The following list describes some of the typical challenges students face if their conceptual understanding of fractions is not well developed.
- Consider the symbol 3/4. This number is made up of two parts, the numerator and the denominator, each represented by a whole number with a specific meaning or value. The denominator tells us that the whole is divided into 4 equal parts, and the numerator tells us that we are concerned with 3 of these parts. In addition to understanding these two values, a student must understand that the symbol 3/4 also represents a single number with a unique value and position on the number line. In other words, to understand the meaning of a single fraction a/b, students must understand the meaning of three numbers: a, b, and a/b. This represents a major conceptual leap from previous work with whole numbers.
- Students learn in the whole number system that 4 is less than 6. However, when comparing the fractions 1/4 and 1/6, 1/4 is larger than 1/6. Students may have difficulty with the idea that the more parts a whole is divided into, the smaller each part is. The following sample dialog between a teacher and student illustrates this confusion (Post et al., 1985):
Teacher: One-fifth and one-eighth—which is less?
Student: One-fifth is less, because five is less than eight.
[The teacher directs the student to use colored pieces to illustrate.]Student: [Covers one circular unit with green (1/5) pieces and another with blue (1/8) pieces, as shown in Figure 4.] It takes 8 blue and 5 green.
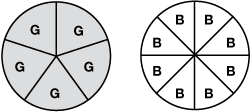
Figure 4: Two fraction circles illustrating fifths and eighths Teacher: [Draws attention to colored pieces] Which is less, one-fifth or one-eighth?
Student: One-fifth, because it takes five to cover this, and it takes eight to cover this [points to the circular units].
One green is bigger than one blue. One-fifth is less than one-eighth. - The previous dialog also illustrates the difficulty many students have with the language we use as we teach fractions. For example when we ask, “Which fraction is less?” do we mean which is less in absolute quantity or do we mean which is a smaller portion relative to the whole? Likewise, when asking, “Which is greater?” are we asking which fraction covers a greater area of the whole or which fraction results in a greater number of parts?
- As students begin to compare and order fractions, their understanding of the whole number system is further challenged. When students order fractions with like denominators, they use the numerators to order the fractions. Ordering fractions using the numerator has a direct relationship to the whole number system. That is, 1/4 < 2/4 < 3/4 < 4/4. However, when students compare and order fractions with like numerators, this relationship changes. Students use the denominators to order fractions, finding that 2/8 < 2/5 < 2/3. When both the numerators and denominators are different, students must have a solid understanding of fractions so they can choose efficient and flexible strategies to compare the fractions.
- The size and shape of a fraction also depends on the unit whole. One-fourth of a round layer cake is a different shape and size than one-fourth of a rectangular sheet cake. Both of these are different from one-fourth of the apples in a bag. Students need to be able to think about the unit whole flexibly, so they can think about the fractional parts flexibly as well. They need to be able to visualize one-half of a pie, one-half of a semicircular patio, and one-half of the eggs in a carton.
- Students can also become confused with counting issues when working with fractions. For example, when you count using whole numbers, you know that 1 comes before 2 and 3 comes after 2. However, when counting with fractions it is difficult to know what comes next. For example, what fraction follows 1/2 on the number line?
Each of these misconceptions can affect a child's understanding of fractions and subsequent ability to use them correctly. Students need experiences in the classroom that will help them develop a strong conceptual understanding of fractions.
Use of Multiple Representations to Support Conceptual Development
The careful development of the fraction concepts in this unit through the use … read more
Use of Multiple Representations to Support Conceptual Development
The careful development of the fraction concepts in this unit through the use of multiple representations and real-world contexts supports all learners. Encouraging students to develop strong visual images of fractions with fraction circle pieces, number lines, and drawings will provide the foundation that they need to make sense of computation with fractions. With this understanding, they will make fewer errors and be better able to judge if their solutions to problems involving fractions are reasonable.
It is important to make the various models available to students throughout the unit as they solve problems in the lessons and Daily Practice and Problems. This is true both for students who struggle with the concepts and those who seem to grasp them easily. Encouraging students to use the models to solve problems will give struggling students the confidence and support they need to learn the content. Asking more advanced students to justify their solutions using the models and to make connections between them will deepen their understanding and provide evidence that they truly understand the concepts.
“Instructional practices that tend toward premature abstraction and extensive symbolic manipulation lead students to have severe difficulty in representing rational numbers with standard written symbols and using the symbols appropriately.”
National Research Council, 2001, p. 234
MATH FACTS and MENTAL MATH

This unit continues the review and assessment of the division facts to develop mental math strategies, gain … read more
This unit continues the review and assessment of the division facts to develop mental math strategies, gain proficiency and to learn to apply multiplication strategies to larger numbers. Students will focus on the division facts for the 9s.
Resources
- Cramer, K., M. Behr, T. Post, and R. Lesh. Rational Number Project: Fraction Lessons for the Middle Grades—Level 1 <http://cehd.umn.edu/rationalnumberproject/rnp1.html>. Kendall Hunt Publishing Co., Dubuque, Iowa, 1997.
- Cramer, K., T. Post, and R. delMas. “Initial Fraction Learning by Fourth- and Fifth-Grade Students: A Comparison of the Effects of Using Commercial Curricula with the Effects of Using the Rational Number Project Curriculum.” Journal for Research in Mathematics Education, 33(2), pp. 111–144, March 2002.
- Cramer, K., and T. Wyberg. “Efficacy of different concrete models for teaching the part-whole construct for fractions.” Mathematical Thinking and Learning, 11(4), pp. 226–257, October 2009.
- Curcio, F.R., and N.S. Bezuk. Understanding Rational Numbers and Proportions. National Council of Teachers of Mathematics, Reston, VA, 1994.
- Curcio, F.R., series editor. Curriculum and Evaluation Standards for School Mathematics, Addenda Series 5–8: Understanding Rational Numbers and Proportions. National Council of Teachers of Mathematics, Reston, VA, 1994.
- Lamon, S.J. “Chapter 2: Fractions and Rational Numbers.” In Teaching Fractions and Ratios for Understanding: Essential Content Knowledge and Instructional Strategies for Teachers. Lawrence Erlbaum Associates, Mahwah, New Jersey, 2006.
- Mack, N.K. “Learning Fractions with Understanding: Building on Informal Knowledge.” Journal for Research in Mathematics Education, 21(1), pp. 16–32, January 1990.
- National Council of Teachers of Mathematics. Principles and Standards for School Mathematics. NCTM, Reston, VA, 2000.
- National Research Council. “Developing Proficiency with Other Numbers.” In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, D.C., 2001.
- Post, T., I. Wachsmuth, R. Lesh, and M. Behr. “Order and Equivalence of Rational Numbers: A Cognitive Analysis.” Journal for Research in Mathematics Education, 16(1), pp. 18–36, January 1985.
- Post, T.R., ed. Teaching Mathematics in Grades K–8, Research-Based Methods. Allyn and Bacon, Boston, 1992.
- Wu, Hung-Hsi. Chapter 2: Fractions (Draft) (June 20, 2001; Revised September 3, 2002).











