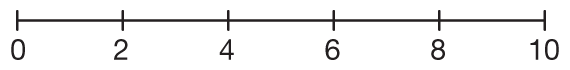Place Numbers on the Number Lines.
Number Lines and Fractions. In this lesson, students use number lines to represent fractions. This reinforces the fact that fractions are numbers, just as whole numbers are. Students often think of a fraction as two separate numbers, a numerator and a denominator, and working with number lines helps overcome this misconception. The number line also provides a visual representation of numbers in increasing order that helps students understand the relative size of fractions.
Completing DPP Bit M as a class is a good way to begin this lesson. Students skip count by fourths from 1 to 5. First they count using mixed numbers, then they count by fourths using improper fractions.
An important concept is that all numbers have a place on the number line even if they are not labeled. To help develop this concept, draw a number line on which not all whole numbers are labeled. For example, draw a number line from 0 to 10 that shows only even numbers, as in Figure 1.
Ask questions that help students understand that the number line has positions for all numbers, such as:
- Are there numbers greater than 10 on the number line? How far does the number line go? (It goes on forever.)
- Skip count by 2s to show how this number line would continue. (0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, and so on.)
- Are there any numbers you can label on the number line between the numbers I have written? (Yes, you can label the odd numbers.)
- Where do the odd numbers belong? Come and write them on the number line. (Put 1 between 0 and 2, put 3 between 2 and 4, and so on.)
- Where can you put the fraction 1/2 on this number line? Show the class. (It goes halfway between 0 and 1.)
- How about 11/2 ? (Put 11/2 halfway between 1 and 2.)
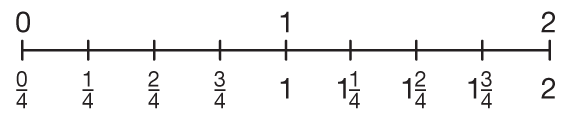
Next, draw a number line from 0 to 1. Divide the segment into four equal parts by making equally-spaced marks between 0 and 1, as in Figure 2.
Help students label the number line by asking:
- Here is a number line from 0 to 1. What fraction of the line is each part? (one-fourth)
- How should we label the first mark after zero? (Write 1/4 beneath the first mark.)
- Where should we write 2/4 ? (at the mark that is 2/4 of the distance from 0 to 1)
- Are there numbers greater than 1 on the number line? (yes)
Extend the number line to 2 as shown in Figure 3 and ask a volunteer to continue writing fractions for fourths. Students may use mixed numbers or improper fractions.
Connect Fraction Strips and Number Lines. Ask students to look at the rectangle on the first page of the Fractions on Number Lines pages in the Student Guide. The rectangle and the number line beneath it each show sixths.
To help them compare the rectangle and the number line, ask:
- What does the rectangle divided into strips look like? (a fraction strip)
- How are the rectangle and the number line alike? (Both are divided into the same number of equal parts. The ends of each part of the rectangle match the ends of each part of the number line.)
- How are they different? (The parts of the rectangle are all labeled the same. Each is labeled 1/6. But on the number line, the labels count up 0/6, 1/6, 2/6, 3/6, 4/6, 5/6, 6/6.)
- Do the labels mean the same thing? (No, the labels on the rectangle show how big each part is. They show that each part is 1/6 of the whole rectangle. The labels at the marks on the number line show what fraction of the distance from 0 to 1 each mark is.)
Have students work on Question 1 in the Student Guide with partners, then discuss with the whole class. Students must decide how to label the number lines based on the number of equal parts into which the interval from 0 to 1 is divided.
Fractions Greater Than One. The figure above Question 2 in the Student Guide shows how to represent fractions greater than one using rectangles and number lines. Point out that the three rectangles together are similar to placing three whole fraction strips together end to end. Have students use the figure to count from 0 to 3 by fifths, first using mixed numbers (Question 2A) and then using improper fractions (Question 2B).
For Question 3, students name points on number lines. Have students discuss their answers with partners before reviewing them as a class.