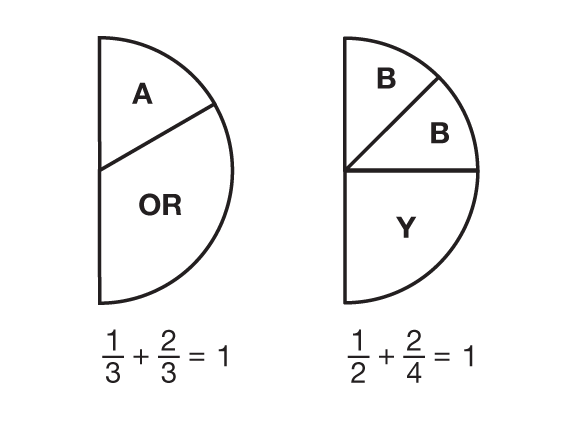Solve Puzzle A. Give each group a set of clues for Puzzle A. Each student should receive one clue. Remind students that they may share their clues with other members of their group only by reading the clue aloud.
This activity works best in groups of four. However, if you have a group of three, give one student two clues to read. If you have a group of five, one student can act as the judge for the group, checking the final solution to make sure it meets all of the guidelines as specified in the clues. On the next puzzle, the role of judge will switch to a different student in the group.
Once a group has a solution that they feel satisfies all of the clues, they record their work by sketching their solution and writing a number sentence that represents it. Two solutions for Puzzle A are shown in Figure 2.
As groups work, observe how they are coming to their answers and encourage them to solve it a second way. When groups have found one or two solutions, ask students to share their solutions with the whole class.
- Show how your solution matches each clue.
- Explain the process you used for solving the problem.
The sample dialog includes prompts for discussing possible solutions and for using language that helps students think of the pink piece as the unit whole.

Teacher: Explain how you solved Puzzle A.
Shannon: We got out a pink piece and tried some different pieces until we found ones that covered it and fit the puzzle.
Teacher: Did anyone start a different way? [Waits for possible response.] Did anyone cover the whole pink piece in one color first?
Jerome: We covered a pink piece with all aquas first.
Teacher: If you cover the whole pink piece with aqua pieces, what fraction of the pink piece does one aqua cover?
Jerome: 1/3 of the pink piece.
Teacher: How can covering the pink piece with 3 aquas help you solve the puzzle, if one of the clues is to use two colors?
Jerome: Cover the whole piece with 3 aquas. Then, you can trade the pieces you need to fit the other clues. You can trade two aquas for one orange piece. Then the number sentence is 1/3 + 2/3 = 1.
Teacher: What other colors can you use to cover the whole pink piece with one color? How many of each piece do you need?
Ming: 2 yellows.
Nila: 4 blues.
Teacher: Nila, can you use Jerome's method to solve the problem, but use blues?
Nila: You mean start with four blues? [Teacher nods.] Well, four blue pieces cover the whole pink piece, so . . . one blue is 1/4. You need to trade one yellow for two blues. One yellow is half the pink piece, so the number sentence is 1/2 + 2/4 = 1.

One strategy for sharing solutions is to pair two groups together. As each of the groups finish, they share their solutions with their partner group before showing it to you or recording it on paper.
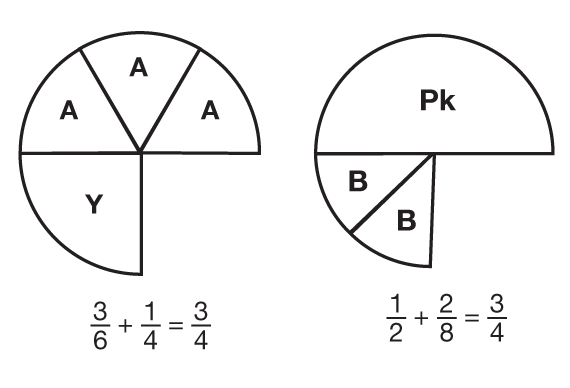
Solve Puzzle B. Distribute the clues for Puzzle B to each group and ask each group member to read one clue. As they work, talk with the groups about their strategies and solutions. Sample solutions for Puzzle B are shown in Figure 3.
Choose one or two groups to share their solutions using discussion prompts similar to those for Puzzle A. Choose solutions from other groups and challenge the class to build the puzzle solutions from the number sentences. For example, write the following on the board:
3/6 + 1/4 = 3/4
- Use your pieces to show how to solve Puzzle B using this solution. (See Figure 3.)
- Show how this puzzle solution matches each clue. (Possible response: The red circle equals one whole and you can show that the solution covers 3/4 by covering it with three yellow pieces. There are two different colors and more than 3 pieces.)
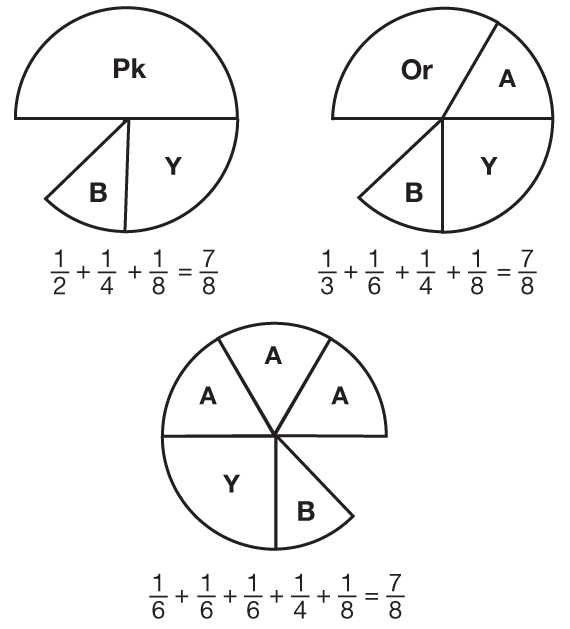
Solve Puzzle C. Distribute the clues for Puzzle C. Possible solutions are shown in Figure 4. Repeat the procedure for solving and discussing the solutions as for Puzzles A and B.

Thinking flexibly about the unit whole. For Puzzle A, the pink piece is one whole. Student work from field test classrooms has shown that some students have difficulty picturing any piece but the red circle as the unit whole. They identify the other pieces in relationship to the red circle instead of the designated whole. These students incorrectly assume that the orange piece is always 1/3 and an aqua is always 1/6. Students who use this thinking may correctly solve Puzzle A by covering a pink piece with an orange and an aqua, but erroneously write: 1/6 + 1/3 = 1 as the number sentence.
To help students think flexibly about the unit whole, remind them that for this puzzle they need to think about the pink piece as the whole and the remaining pieces as fractions of the pink piece. Use questions such as:
- How many aquas cover the pink piece? How many aquas cover the unit whole? (3)
- What fraction of the pink piece is an aqua? (1/3)
- If an aqua is 1/3 of the pink piece, then what fraction of the pink piece is an orange? (1/2)
- Use these fractions in your number sentence.