Lesson 10

Multiplying Fractions by a Whole

Est. Class Sessions: 2–3

Developing the Lesson

Part 3. Fractions of Groups

Identify the Whole Group. In Parts 1 and 2, students explored fractions using area models and a number line model. In Part 3, students work with fractions of sets of discrete objects. For example, students find the fraction of red apples in a box of 12 apples. The whole is a group of 12 discrete objects. The sequence of discussion questions develops the fraction concepts involved in multiplying a fraction and a whole number. Arrays of apples in different-sized gift boxes provide the context.

Note that while the word “of” often implies multiplication, it is important not to overgeneralize. For example, the problems below use the word “of” but are solved without multiplication:

Six of the students in Mr. Moreno's class are learning to play instruments, and eight of his students are in the chorus. How many are studying music?

If there are 22 students in Mr. Moreno's class, what fraction of the students are learning to play an instrument?

Use Questions 7–11 in the Fractions of Groups section in the Student Guide to lead a discussion.

Students investigate the concept of a whole in Questions 7–8. Just as the size of a fraction using an area model depends on the area of the whole, the size of a fraction of a set of discrete objects depends on the number of objects in the whole set. First, students find the number of apples in two different-sized gift boxes. One-fourth of the apples in a box of 12 apples is three apples (Question 7A), while one-fourth of a box of 24 apples is six apples (Question 7B).

Question 8 reviews the terms numerator and denominator. For the fraction 1/4, the 4 in the denominator tells us to divide the 12 apples into four equal groups. The 1 in the numerator tells us that we are interested in one of the groups. To know the number of apples in 1/4 of a box of apples, it is essential to know the number of apples in the whole box (Question 8C). To show the difference between the meaning of the fractions 1/4 and 4/1 (Question 8D), we can apply the definitions of numerator and denominator to 4/1. For the fraction 4/1, the 1 in the denominator tells us that all of the apples in the whole set are in one group. The 4 in the numerator means that we are interested in 4 whole groups, so 4/1 is equivalent to 4 whole boxes.

Questions 9–11 emphasize the language used in multiplication sentences. A number sentence for “Four groups of 6 apples makes 24 apples in all” is 4 × 6 = 24. Similarly, a number sentence for “One-fourth of a group of 24 apples is 6 apples” is 1/4 × 24 = 6.

Ask students to write number sentences for the following:

How many players are on 8 teams of 11 players each? (8 × 11 = 88)
One-half of a class of 22 students goes home for lunch. How many students go home for lunch?
(1/2 × 22 = 11)

Estimate Products of Fractions. Display the following problems:

1/6 × 12 6/6 × 12 9/6 × 12

1/3 × 12 2/3 × 12 6/3 × 12

Give students a few minutes to solve each problem and ask:

Which products are greater than 12? Explain.
(9/6 × 12, 6/3 × 12; Possible response: 9/6 × 12 is greater than 12. 6/6 × 12 = 12 so 9/6 × 12 is more than 12 because there are more than 6 sixths.)
Which products are less than 12? Explain.
(1/6 × 12, 1/3 × 12; Possible response: the fraction is less than 1 so the product will be less than 12. 1/6 × 12 = 2 and 1/3 × 12 = 4.)
Which products are equal to 12? Explain.
(6/6 × 12, 3/3 × 12; Possible response: 6/6 and 3/3 both equal 1. 1 × 12 = 12.)
Do you see a pattern that would help you estimate a product?

A diagram is used in the Student Guide to solve the problem 4/3 × 12 = 16. Ask students if they can solve the problem another way. They may see that since 4/3 equals 11/3, the problem can be rewritten as 11/3 × 12. Remind students that 11/3 can be thought of as 1 and 1/3 or 1 + 1/3. Using the context of the apple gift boxes, we can find the number of apples in one whole box (12) and the number of apples in 1/3 of a box (4) and reason that one and one-third boxes of apples is 12 + 4, or 16 apples.

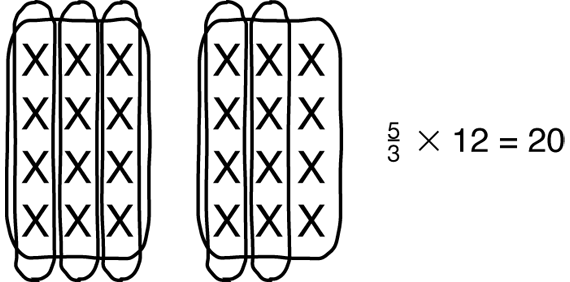
To complete the row for 5/3 × 12, students can draw a diagram similar to the one in Figure 2 which shows two whole sets of 12 apples. Each set is divided into three groups, and five of the groups are circled, so 5/3 × 12 = 20.

Ask student pairs to complete Questions 12–13 together. Questions 12–13 develop students' number sense so that they will be able to estimate the product of a fraction and a whole number. Students use diagrams of sets to complete the table in Figure 3.

Question 13A asks students to look for patterns in the table. Possible student responses include the following:

As the fraction gets larger, the product gets larger.
You can find the products by skip counting by fours since 1/3 of 12 is 4.
When the fraction is less than one, the product is less than 12.
When the fraction is greater than one, the product is greater than 12.

Question 13C asks students when the product of a fraction and 12 is equal to 12. The product is equal to 12 when the fraction is 3/3 or 1. This is because multiplying a number by one results in the same number.

After discussing the patterns in the products, assign Questions 14–15 to practice estimating and finding products of fractions and whole numbers.

Assign Questions 4–10 from the Homework section in the Student Guide after Part 2.