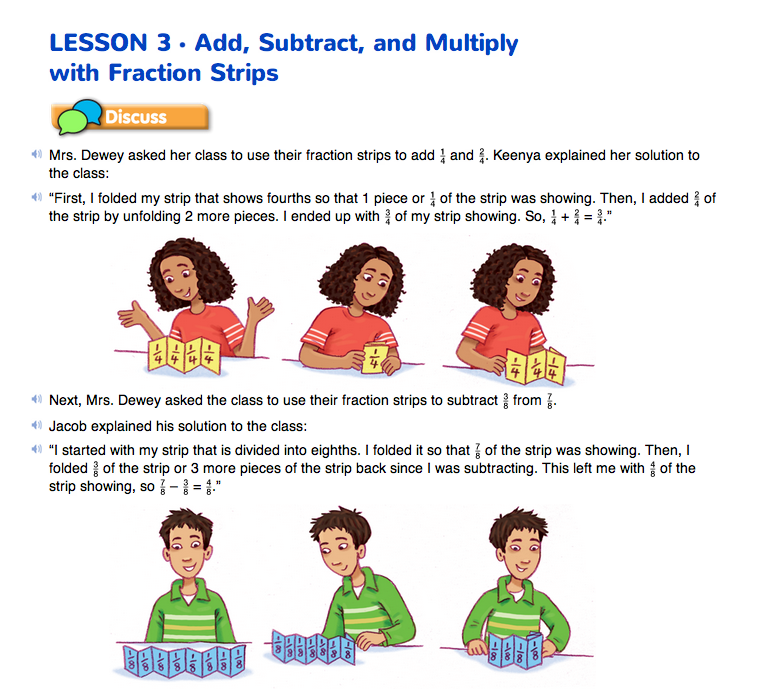
Use Fraction Strips to Solve Problems. Introduce this lesson by reading the vignette on the Add, Subtract, and Multiply with Fraction Strips pages in the Student Guide with the class.
Ask students to work in groups of three to act out the vignette. One group member plays the role of Mrs. Dewey and two other members play the two students, Keenya and Jacob, who demonstrate how to add and subtract using the fraction strips. Then ask one group to demonstrate each students' solution for the whole class.
On the board or chart paper, begin a class list of the number sentences students write to solve the problems in this lesson. Ask the students who played Keenya and Jacob to begin the list by writing their number sentences large enough for the class to see. See Figure 1. Students will revisit this list during the lesson summary.
Discuss Keenya's and Jacob's solutions.
Use prompts similar to the following:
- Is Keenya's answer reasonable? Does it make sense? Why or why not? (Possible response: You can see it with the strips. Each folded part is one-fourth and when you put them together you have three parts, so that's 3/4.)
- What does the denominator tell you in Keenya's number sentence? (Possible response: I know to use the yellow strip because it shows fourths.)
- How many equal parts is the yellow strip divided into? (4 parts)
- What do the numerators tell you in Keenya's sentence? (how many parts to put together)
Use Strips to Solve Problems. Ask students to solve Questions 1–7 in the Student Guide with partners.
Note that two sets of fractions strips are needed for Questions 5–7. As students work together in pairs, talk with them about their work. Use questions similar to the discussion prompts above to draw attention to the role of the numerators and denominators in number sentences. Ask them to use their fraction strips to show you how they solved the problems.
Sample discussion prompts for the problems follow:
- What number sentence did you write for Question 1? (5/8 − 3/8 = 2/8)
- Show me with your fraction strips how your number sentence matches how you solved the problem. (Possible response: I started with a blue strip with 5 parts showing. That's the 5/8. Then I folded back 3 parts for subtracting 3/8. Two parts are left showing. That's the answer, 2/8.)
Both Questions 2 and 3 reinforce the concept that when the numerator and the denominator are the same number, the fraction indicates one whole. In Question 2, students use their fourths strips to add 1/4 and 3/4. Show students the following two number sentences and ask if they are both correct:
1/4 + 3/4 = 4/4 or 1/4 + 3/4 = 1
Students should see that they are both right, because 4/4 is the same as 1.
Ask students to use their fraction strip to show why 4/4 is the same as 1 whole.
- Explain what the numerator and denominator mean in 4/4. (Possible response: The strip is divided into 4 equal parts. That's the 4 in the denominator. 4/4 in the answer means that you need all 4 parts. The 4/4 strip is the same as the one whole strip.)
- How did you start Question 3? What strip did you use? (Possible response: We used the twelfths strip because you are supposed to subtract 5/12.)
- How did you use the twelfths strip? What does it represent in the problem? (We started with the whole strip because Jessie started with a whole board.)
- How many twelfths are in one whole? (twelve twelfths)
- Can you write two number sentences for this problem? (1 − 5/12 = 7/12 and 12/12 − 5/12 = 7/12)
- How did you start Question 4? What does the strip represent? (Possible response: I used the sixths strip and folded back one part so it shows 5/6. That stands for 5/6 of the pie left on the counter.)
- What do the denominator and numerator in the phrase “5/6 of a pie left on the counter” tell you about the pie? What does the numerator tell you? (The pie was cut in 6 equal pieces. There are 5 pieces left in the pan.)
- How does that match your strip? (There are six equal pieces on the strip and 5 are left showing.)
- How did you show the fractions of the pie that Luis and his sister ate in Questions 4A and 4B? (I folded back 2/6 for the fraction Luis ate and then another 1/6 for the fraction that his sister ate.)
- What fraction is left? (2/6)

Talking with students as they work provides opportunities to adapt questions for students who are either struggling or moving quickly. Use the prompts in the lesson and those below to develop questions for your students.
For students who are struggling, ask:
- What strip will you use to start this problem? What does it represent in the problem?
- What fraction will you start with? How will you show it?
- How will you show addition (subtraction) using your strips?
- How do the numbers in your sentence match the problem? Show me with your strip.
For students who are moving quickly through the problems, begin with the final question in the list above to check for understanding. Then continue with more challenging questions:
- How do the numbers in your sentence match the problem? Show me with your strip.
- Can you write a different number sentence that matches the problem?
- Write two problems that another student can solve using the fraction strips. Choose something you know about that involves the fractions represented by the strips. Be sure the fractions in your problems have the same denominator. Write the problem and an answer as a number sentence. Trade your problems with another student and solve them.
- Write the four number sentences in the “fact family” for Questions 7A and 7F. (For Question 7A: 3/8 + 2/8 = 5/8, 2/8 + 3/8 = 5/8, 5/8 − 3/8 = 2/8, 5/8 − 2/8 = 3/8)
- Find a way to use your strip to solve these problems:
1/2 + 1/4
3/4 − 1/2
1/3 + 1/6
1/2 − 1/6
Note that it is not necessary for students to first find a common denominator to add or subtract the fractions. Students can solve the problems with the fraction strips and write number sentences with or without the common denominators. This helps students develop a strong visual image of the addition and subtraction operations along with number sense for the size of the fractions in the answers without relying on rules that do not yet make sense to them.
Question 4C asks students to use their fraction strips to find an equivalent fraction to 2/6.
- How can you use your fraction strips to find a fraction equivalent to 2/6? (Use the other strips to compare and find fractions that are the same size.)
- How many can you find? What are they? (three; 1/3, 3/9, 4/12)
Students will need to work with a partner to solve Questions 5–7. In Question 5, each student will need to use his or her tenths strip. After adding 8/10 and 8/10, students should find that Ming's total trip was 16/10 miles. Some students may recognize this as 16/10 miles; however, not all students will make this connection. Changing improper fractions to mixed numbers will be studied in fifth grade. It is not necessary that students do this at this time. The possible number sentences for Question 5 are 8/10 + 8/10 = 16/10 or 8/10 + 8/10 = 16/10.
To complete Question 6, each pair of students will need to use both of their fourths strips. After adding 3/4 and 2/4, students should find that Irma must wait 5/4 hours before going outside. Students may recognize this as 11/4 hours. The possible number sentences for Question 6 are: 3/4 + 2/4 = 5/4 or 3/4 + 2/4 = 11/4. Either sentence is acceptable. Question 7 asks students to add and subtract fractions with like denominators in number sentences. Adapt the Show Me game from Lesson 2 to provide targeted practice with adding and subtracting and representing fractions.
Share Solutions. Ask students to share their solutions to Questions 1–7. As volunteers discuss the solutions, ask them to write some of the number sentences for the addition and subtraction problems on the class list started at the beginning of the lesson. See Figure 1.
Assign Check-In: Questions 8–11 in the Student Guide.
Ask students to use their fraction strips to complete Check-In: Questions 8–11 in the Student Guide individually or in pairs. These problems can be used to assess students' progress toward adding and subtracting fractions with like denominators using area models [E10] and represent fractions [E5].
Adapt the Show Me game from Lesson 2 to provide targeted practice with adding, subtracting, and representing fractions.