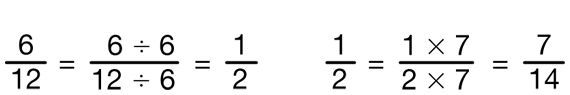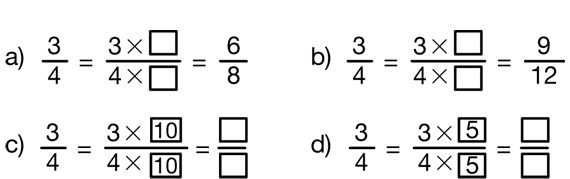Equivalent Fractions
Est. Class Sessions: 2–3Developing the Lesson
Part 3. Finding Equivalent Fractions
Use Multiplication and Division Strategies to Find Fractions Equivalent to 1/2. In Questions 8–10 in the Finding Equivalent Fractions section in the Student Guide, students will begin to develop multiplication and division strategies for finding equivalent fractions by first identifying the patterns they find in the numerators and denominators of equivalent fractions. Before assigning these questions, display the list of equivalent fractions students found in the first part of this lesson. See Figure 2. Ask students to work with a partner to complete Question 8 and then use the following prompts to guide a discussion.
Ask:
Assign Question 9 that asks if 1/2 = 50/100 and ask students to share their solutions.
Based on Jerome's problem, ask students to name other fractions that are equal to 1/2. Evaluate each student suggestion, adding those that are appropriate to the list of equivalent fractions created at the start of the lesson.
Write the following number sentences on the board along with some of the fractions suggested by the students:
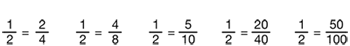
Ask students to look for a pattern in the number sentences. Start with looking at just a few of the number sentences.
Ask:
Write the following number sentences on the board:
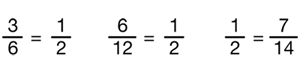
Ask:
If no one suggests the pattern, use one or two number sentences and help students see that the numerator and denominator are both multiplied (or divided) by the same number to get the equivalent fraction.
Ask:
The pattern is shown in Figure 3.
In Question 10, Nila uses this pattern to find two fractions equivalent to 1/2. Provide time for students to study Nila's method for finding equivalent fractions and then ask students to share their explanations of her method and how she used it to find another fraction equivalent to 1/2.
Use Multiplication and Division Strategies to Find Other Equivalent Fractions. Continue exploring this pattern by assigning Question 11, in which students find fractions equivalent to 3/4. Once students have used the fraction circle pieces to find fractions equivalent to 3/4, write the related number sentences as shown in a) and b) in Figure 4.
Ask:
Have students suggest numbers to multiply by to find two more equivalent fractions.
Ask:
After completing the discussion for Question 11, have students work with a partner or in a small group to complete Questions 12–17. For Questions 12A and 13A, students will be able to use the circle pieces to find two equivalent fractions. However, this will not be possible for Questions 12B and 13B since there are no more equivalent fractions represented in the set of circle pieces. Students will have to use other methods to find equivalent fractions. Suggest they draw pictures or write number sentences. Use Figure 4 and Nila's method as a model. Evaluate students' suggestions of equivalent fractions to see if they are equivalent and ask them to explain their thinking.
In Question 14, students explore one strategy for finding equivalent fractions in which the top and bottom cannot be multiplied by a whole number to complete the number sentence. For example, 2/8 = 5/20.
Jackie finds an equivalent fraction to 2/8 that is simpler, 1/4. Then she finds an equivalent fraction for 1/4 that will also be equivalent to 2/8. The diagram shows another way of looking at the process: by dividing the 1/4 part into 5 equal pieces, she is essentially multiplying the numerator by 5. Then, to determine how many of that size piece are in the whole, each of the remaining fourths must also be divided into 5 equal pieces. This results in the whole now being divided into 20 total pieces. One-fourth is 5 parts (numerator) out of the total 20 parts (denominator).
In Questions 15 and 16, students use the relationship between the numerator and denominator to determine if fractions are equivalent. Students use all these strategies to find equivalent fractions in Question 17.
Find Missing Numerators and Denominators. Before assigning Question 18, ask students to complete the number sentences below:
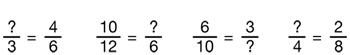
Ask:
Students may suggest using multiplication as a strategy. For example, to find the missing number in the sentence ?/3 = 4/6, students may say: “Since you multiply 3 by 2 to get the denominator of 6, what number would you multiply by 2 to get the numerator of 4? Since 2 times 2 equals 4, the missing numerator is 2.”
Other students may suggest using division as a strategy. For example, in the number sentence 10/12 = ?/6, they may say, “Since you divide 12 by 2 in order to get 6, you must also divide 10 by 2. This gives a numerator of 5.”
Students may also use the fraction circle pieces to solve or verify their solutions.
Provide students an opportunity to share the strategies used to complete the number sentences in Question 18. Note that Question 18H cannot be solved by multiplying or dividing by a single number. Rather, suggest to students that they review Jackie's strategy in Question 14.
Assign the homework section of the Equivalent Fractions pages from the Student Guide.