Lesson 4

Comparing Fractions

Est. Class Sessions: 1

Developing the Lesson

Make Fraction Charts.

Pose the following question:

Jerome has 2/3 yard of ribbon and Shannon has 1/2 yard of ribbon. Who has more ribbon?

Have students suggest possible strategies. If it is not mentioned, suggest using fraction strips.

Ask a student to demonstrate the relative size of the two fractions using his or her fraction strips.

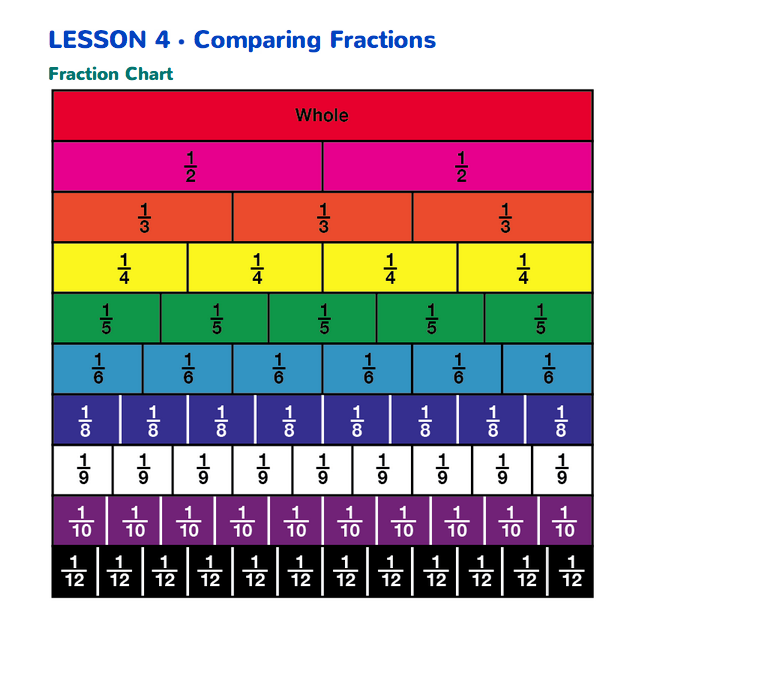
Students make a chart from their strips so they can easily compare the sizes of different fractions. Each student needs a complete set of fraction strips (from Lessons 1 and 2) and a blank sheet of paper. To make the chart, students should first experiment with organizing the strips so the charts will be useful for comparing fractions.

Ask two or three students:

How did you decide to order your fraction strips?
How will the order help you compare fractions?

Students may decide to organize their charts from top to bottom in descending order from the largest-sized piece to the smallest-sized piece. An example of this is shown in Figure 2. Other students may choose to organize their charts by placing the strips in groups of related fractions. See Figure 3.

Students will then glue their strips to blank sheets of paper in the order they choose. The only guidelines all students must follow are:

Be prepared to explain the order of your strips.
Place the strips so that long edges line up one against the other.
Glue strips down so they are touching each other. This makes it easier to compare fractions.
Line up the left and right edges of all of the strips.

The ten fraction strips will fit on an 81/2 × 11–inch sheet of paper, if they are placed as shown in Figures 1 and 2. To help students line up their strips so they are straight, suggest that they align their first strip along the top edge of their papers. They can also match either the right or left edge (short edge) of their strips with the edge of their papers.

Once students have completed their charts, they can use them to complete Questions 1–12 on the Comparing Fractions pages in the Student Guide. A copy of the Fraction Chart is in the Student Guide, but it is smaller than the students' charts. Students need to keep their fraction charts for use as a reference in later lessons of this unit.

After students complete the Comparing Fractions pages, provide an opportunity for them to share their work.

Compare Fractions to 1/2. Question 3 asks students to use their Fraction Charts to name fractions that are greater than, equal to, and less than 1/2. As you discuss their answers, make a list of fractions in each category on the board. Question 4 asks them to describe a pattern that helps them compare a fraction to 1/2.

To help them think about this, ask:

Name fractions that are the same size as 1/2.
(2/4, 3/6, 4/8, 5/10, 6/12)
What is the name we give fractions that are the same size or equal? (equivalent fractions)
How can you tell when a fraction is equivalent to 1/2? (The numerator is exactly half of the denominator. The denominator is twice the numerator.)
Let's think about why that makes sense. Look at one of your strips. How many pieces will fill up half of a strip? (half of the number of pieces the strip is divided into)
If a strip is divided into 12 pieces, how many pieces will fill up half the strip? (6) So six-twelfths is the same as 1/2.
If a strip is divided into 8 pieces, how many pieces will fill up half the strip? (4) So how many eighths are there in 1/2 of the strip? (4)
Is 4/8 equivalent to 1/2? (yes)
If I had a strip that was divided into 14 pieces, how many pieces would fill up half the strip? (7, because 7 is half of 14)
Is 7/14 equivalent to 1/2? (Yes, the numerator is exactly half the denominator.)

After students recognize fractions that are equivalent to 1/2, they extend the patterns to determine whether a fraction is greater or less than 1/2.

Ask:

How can you tell when a fraction is less than 1/2? (The numerator is less than half the denominator.)
How can you tell that a fraction is greater than 1/2? (The numerator is greater than half the denominator.)
Is 3/14 less than or greater than 1/2? (less than, because 3 is less than 7, which is half of 14)
Is 10/14 less than or greater than 1/2? (greater than, because 10 is greater than 7)

The symbols <, =, or > are reintroduced. (See TIMS Tip.) Question 5 gives several more fractions for students to compare to 1/2.

If students are not familiar with the symbols for less than (<) and greater than (>), model this before they answer Question 5.

In Question 6, students use their Fraction Charts and the symbols <, =, or > to complete number sentences comparing fractions.

Write 1/4 + 1/4 1/8 + 1/8 on the board and ask:

Is 1/4 + 1/4 greater than, less than, or equal to 1/8 + 1/8? Show us how you know. (1/4 + 1/4 > 1/8 + 1/8. I know because 1/4 + 1/4 equals 2/4, which is the same as one-half. Eighths are even smaller than fourths, so 2 eighth parts would not be as large as 2 fourth parts.)

Compare Using 1/2. Next, students use 1/2 as a benchmark when comparing the sizes of different fractions. For example, to compare 1/4 to 5/8, first compare each fraction to 1/2. 1/4 is smaller than 1/2 and 5/8 is a little larger than 1/2. Therefore, 1/4 is smaller than 5/8.

Students can practice using 1/2 as a benchmark in Question 7 since each pair of fractions students compare includes one fraction that is less than or equal to 1/2 and one fraction that is greater than or equal to 1/2.

In Question 8, students are asked to determine which number sentences incorporating the symbols <, =, or > are true.

Write 3/6 + 3/6 < 6/12 on the board and ask:

Is 3/6 + 3/6 < 6/12 a true number sentence? Show us how you know. (No. I know 6/12 is the same as one-half, and I know that 3/6 is the same as one-half. But when I add 3/6 to 3/6, it equals one whole, and that is larger than 1/2.)
Rewrite this number sentence to make it true.
(3/6 + 3/6 > 6/12)

Write 3 × 1/9 > 1/3 on the board and ask:

Is 3 × 1/9 > 1/3? (No. 3 × 1/9 is the same as 1/9 + 1/9 + 1/9. That is 3/9. When I use my chart, I see that 3/9 is the same as 1/3, so they are equal or equivalent.)
Rewrite this number sentence to make it true.
(3 × 1/9 = 1/3)

Compare Fractions with the Same Numerator or the Same Denominator. Questions 9 and 10 develop strategies for ordering fractions when the numerators are all the same. Students should see that when all of the fractions have the same numerator, they can order them according to the denominators—the larger the denominator the smaller the fraction. Reinforce this concept by having students refer back to their charts.

Ask:

Why are fractions with larger denominators smaller? Look at Question 9A, where the numerator is 1. Why is 1/6 less than 1/3 ? (The denominator is the number of parts you divide the whole into. The larger the number of parts, the smaller each part will be.)
How about Question 9B, in which the numerators are all 3? Why is 3/5 less than 3/4? (3/5 is three pieces that are each 1/5 of the whole. 3/4 is three pieces that are each 1/4 of the whole. I know that each 1/5 piece is less than each 1/4 piece, so three one-fifth pieces, 3/5, must be less than three one-fourth pieces, 3/4.)

Questions 11 and 12 ask which fraction is smallest when two or more fractions have the same denominator. Remind students to think of the fraction strips as they answer this question. If fractions have the same denominator, they are represented by dividing the whole into pieces of the same size, or by using the same strip. The larger the numerator, the more pieces are represented by the fraction and therefore, the larger the fraction. Reinforce this concept by having students refer back to their charts.

Assign Questions 13–16. When ordering fractions in Questions 13–15, encourage students to use a second strategy to check their answers. For example, students can use 1/2 as a benchmark to order the fractions in Question 13A, then check their work using their Fraction Charts.

Question 16 asks students to use the symbols <, =, or > to compare and complete number sentences, again using 1/2 as a benchmark.