Show Me Fractions Less Than One. When students combine their strips with those they made in the last lesson, they will have a set of strips to show one whole, halves, thirds, fourths, sixths, eighths, ninths, and twelfths. Ask them to lay all eight strips on their desks. Then lead an extended version of the Show Me activity from Lesson 1.
To begin, ask a volunteer to name a fraction that can be represented with one of the strips and ask the class to fold their strips to show the fraction named. Encourage volunteers to use a variety of numerators and denominators. If students have not named them, suggest fractions like the following:
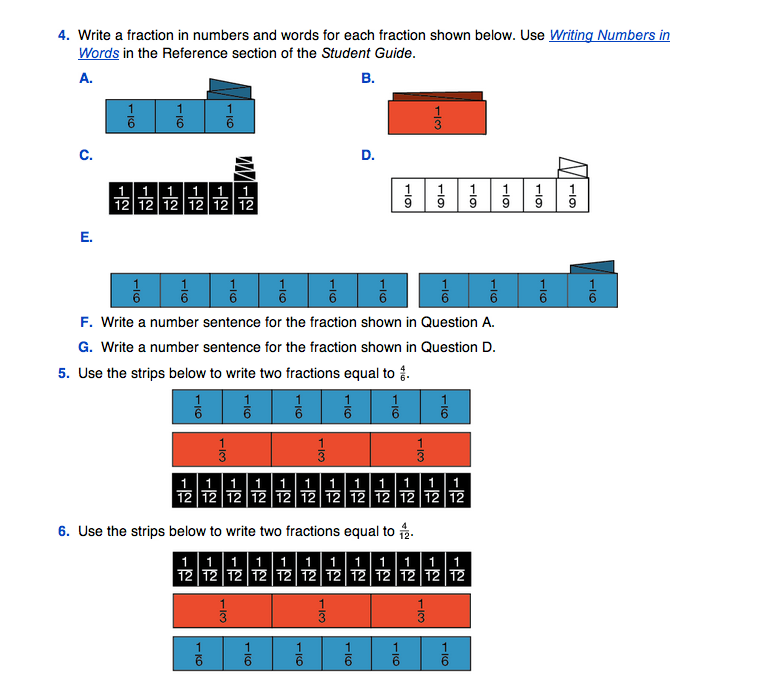
Match the Fraction with Number Sentences and Words. In this lesson, students are asked to name fractions with words and number sentences. Direct students' attention to a display of the Writing Numbers in Words page of the Reference section in the Student Guide. Refer to the Fractions and Decimals section. Show students the examples on the page: 3/4 is written three-fourths, 2/2 is written two-halves.
Next, show students fractions less than one with your thirds, sixths, ninths, or twelfths strips and ask them to name the fraction. Then ask them to write the fraction as a number sentence and in words on the board.
For example, show students your fraction strip for 4/6 and ask:
- Name this fraction. (4/6)
- Write this fraction in words. (four-sixths)
- Write the number sentence that describes this fraction. (1/6 + 1/6 + 1/6 + 1/6 = 4/6)
Students learn to use vocabulary like mixed numbers and improper fractions by using them and talking about them. Early on, encourage students to write a fraction greater than one two ways. As students show these two ways, as an improper fraction or as a mixed number, they will start to use specific words to differentiate between the two representations.
Show Me Improper Fractions and Mixed Numbers. Repeat the Show Me activity, but use fractions greater than one. Use both mixed numbers and improper fractions. Students will need to use two strips to represent these fractions. Examples include:
11/6, 13/12 , 14/12 , 11/6 , 9/9
Students need to recognize that the fractional parts of a unit whole must be equal. Students have been developing this concept since their first exposure to fractions. This is often forgotten when working with new fractions.
After students have participated in Show Me with fractions larger than one, ask them to write fractions as both mixed numbers and improper fractions. For example, ask a pair of students to use two orange strips to show 12/3. Write 12/3 on the board and tell students that it is a mixed number because it has a whole number and a fraction.
- How can I write this number as an improper fraction or using only a numerator and denominator? (5/3)
- What does the denominator tell you? (One whole strip is divided into three equal parts.)
- What does the numerator tell you? (We are interested in 5 parts.)
- Write this fraction in words. (five-thirds)
Ask another pair of students to show 11/9 using their white strips. Write the fraction on the board.
- Is this fraction greater than one or less than one? How do you know? (It is greater than one, because it is made up of one whole strip and some more.)
- How can I write this fraction as a mixed number? (12/9)
- Show how the symbols in the mixed number match the strips.
- Write this fraction in words. (one and two-ninths)
Repeat the activity with other mixed numbers and improper fractions like the following:
4/3, 13/9, 12/6, 15/12
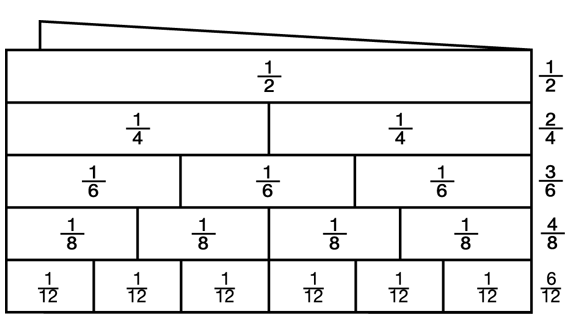
Equivalent Fractions. To help students recognize equivalent fractions, ask students to fold their pink halves strip to show 1/2.
Ask students to look at the other fraction strips they have folded and ask:
- Which strips can you fold to show this part of the whole? (See Figure 4.)
- Name the fractions you can make with your strips that are equivalent or equal to 1/2. (1/2, 2/4, 3/6, 4/8, 6/12)
- What do you notice about the denominators? (They are all multiples of two. They are all 2 times the numerator.)
- Which strip(s) cannot be folded on existing fraction lines to show an equivalent fraction for 1/2? (thirds and ninths)
Connect Repeated Addition to Multiplication.
To make the connection between the repeated addition to multiplication, ask:
- Is this a true number sentence: 1/2 = 1/6 + 1/6 + 1/6? How do you know? (Yes, because both sides of the equation equal the same amount. When I use my strips, I see that three one-sixth parts show the same amount as a one-half strip.)
- Is this a true number sentence: 1/6 + 1/6 + 1/6 = 3 × 1/6? How do you know? (Yes, because both sides of the equation show 3 one-sixths. Multiplication is like repeated addition. I can add one-sixth 3 times, or I can multiply 3 times one-sixth.)
Repeat this activity in a similar fashion with 1/3 and 1/4.
- What are all the fractions that are equivalent to 1/3? (2/6, 3/9, 4/12)
- What do you notice about the denominators? (They are all multiples of 3. They are 3 times the numerators.)
- Is this a true number sentence: 1/12 + 1/12 + 1/12 + 1/12 = 1/3? How do you know? (Yes, because both sides of the equation equal the same amount. When I use my strips, I see that four one-twelfth parts show the same amount as a one-third strip.)
- Is this a true number sentence: 4 × 1/12 = 1/12 + 1/12 + 1/12 + 1/12? How do you know? (Yes, because both sides of the equation show 4 one-twelfths. I can add one-twelfth 4 times, or I can multiply 4 times one-twelfth.)
- What are all the fractions that are equivalent to 1/4?
(2/8 and 3/12)
- Write these in words. (two-eighths, three-twelfths)
- What do you notice about the denominators? (They are all multiples of 4. They are all four times the numerator.)
- How do I know the fractions are equivalent? (The shapes are congruent or the strips are the same length or area.)
- Is 1/4 = 1/8 + 1/8? (yes)
- Is 1/8 + 1/8 = 2 × 1/8? (yes)
- Write an addition sentence to show that 1/4 is equivalent to 3/12. (1/4 = 1/12 + 1/12 + 1/12)
- Write a multiplication sentence to show that 1/4 is equivalent to 3/12. (1/4 = 3 × 1/12)
Suggest other fractions, e.g., 3/4, 5/6, 8/12 , and ask students to find their equivalents.
Students work with partners to answer Questions 1–6 in the Thirds, Sixths, Ninths, and Twelfths section of the Student Guide. They can also complete these problems for homework.