Lesson 1

Multiplication and Rectangles

Est. Class Sessions: 2–3

Daily Practice and Problems

Teacher Notes
X

TIMS Challenge

This problem can be used as a Problem of the Week.

  1. The largest sum is 9753 + 8642 = 18,395. The smallest sum is 1046 + 2357 = 3403 (or 1357 + 0246 = 1603 if leading zeros are allowed). Other addends may give the same sums and are also correct.

    If repeated digits are allowed, the largest sum is 9999 + 9999 = 19,998. The smallest sum is 1000 + 1000 = 2000. If leading zeros are allowed, then the smallest sum is 0000 + 0000 = 0.
  2. The largest difference is 9876 − 1023 = 8853 (or 9876 − 0123 = 9753 with leading zeros). There are three problems that yield the smallest difference: 4012 − 3987 = 25; 5012 − 4987 = 25; 6012 − 5987 = 25.

    If a digit can be used more than once, the largest difference is 9999 − 1000 = 8999 (9999 − 0000 = 9999 using leading zeros). The smallest difference is any number minus itself, e.g., 4563 − 4563 = 0.

    Have students keep a record of the solutions they tried and discarded before reaching their final answers.

D. Biggest and Smallest Sums

  1. Put a digit (1, 2, 3, 4, 5, 6, 7, 8, 9, or 0) in each box. Use each digit once or not at all.
    1. What is the largest sum you can make?
    2. What is the smallest?
    3. What are the answers to A and B if a digit can be used more than once?

      ____________________________________________________________

      ____________________________________________________________
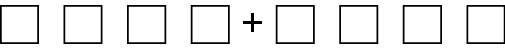
  1. Explain your strategies for Questions 1A–1C on a separate sheet of paper.
  1. Put a digit (1, 2, 3, 4, 5, 6, 7, 8, 9, or 0) in each box. Use each digit once or not at all.
    1. What is the largest difference you can make? ____________________
    2. What is the smallest? ____________________
    3. What are the answers to A and B if a digit can be used more than once?

      ____________________________________________________________

      ____________________________________________________________
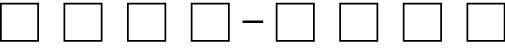
  1. Explain your strategies for Question 2A–2C on a separate sheet of paper.