Lesson 8

Slides, Flips, and Turns

Est. Class Sessions: 2

Daily Practice and Problems

Teacher Notes
X

TIMS Challenge

This can be a Problem of the Week. Let students work at the problem for a day and then give Hint #1. Give Hint #2 midweek to students who haven't solved the problem yet.

Hint #1: What number has to be in the ones place in the answer?

Hint #2: When adding two 2-digit numbers, how do you end up with 3 numbers in your answer?

To solve the problem, students have to access their knowledge of place value.

Step 1: 7 + 7 = 14, so T must be “4”; carry the ten to the tens column.

Step 2: Two 2-digit numbers will add to a 3-digit number only when the sum is 100 or more; with only two addends, the sum cannot be above 200. So “O” has to be “1” (one) in the hundreds place.

Step 3: The first addend also has an “O” so the addend is 17.

Step 4: The second addend has to be 87 or 97 in order to sum to more than 100.

Step 5: Try 17 + 97 = 114. That would mean that “U” is equal to “1” but the rule says that no two letters stand for the same number and we already know that “O” is equal to “1.”

Step 6: That means the second addend has to be 87. 87 + 17 = 104; “U” is equal to “zero.”

N = 7; O = 1 (one); I = 8; U = 0 (zero); T = 4

V. Crack the Code

This is an addition problem. It is solved correctly, but it is written in code. Find out what number each letter stands for. One letter is already solved for you. Here are the rules:

  • Each letter stands for only one number between 0 and 9.
  • Two different letters cannot stand for the same number.
  • The letter N stands for the number 7.

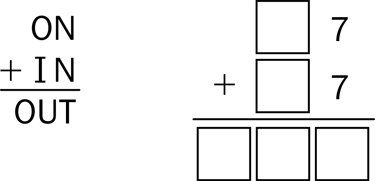
N = 7      O = ________      I = ________      U = ________      T = ________