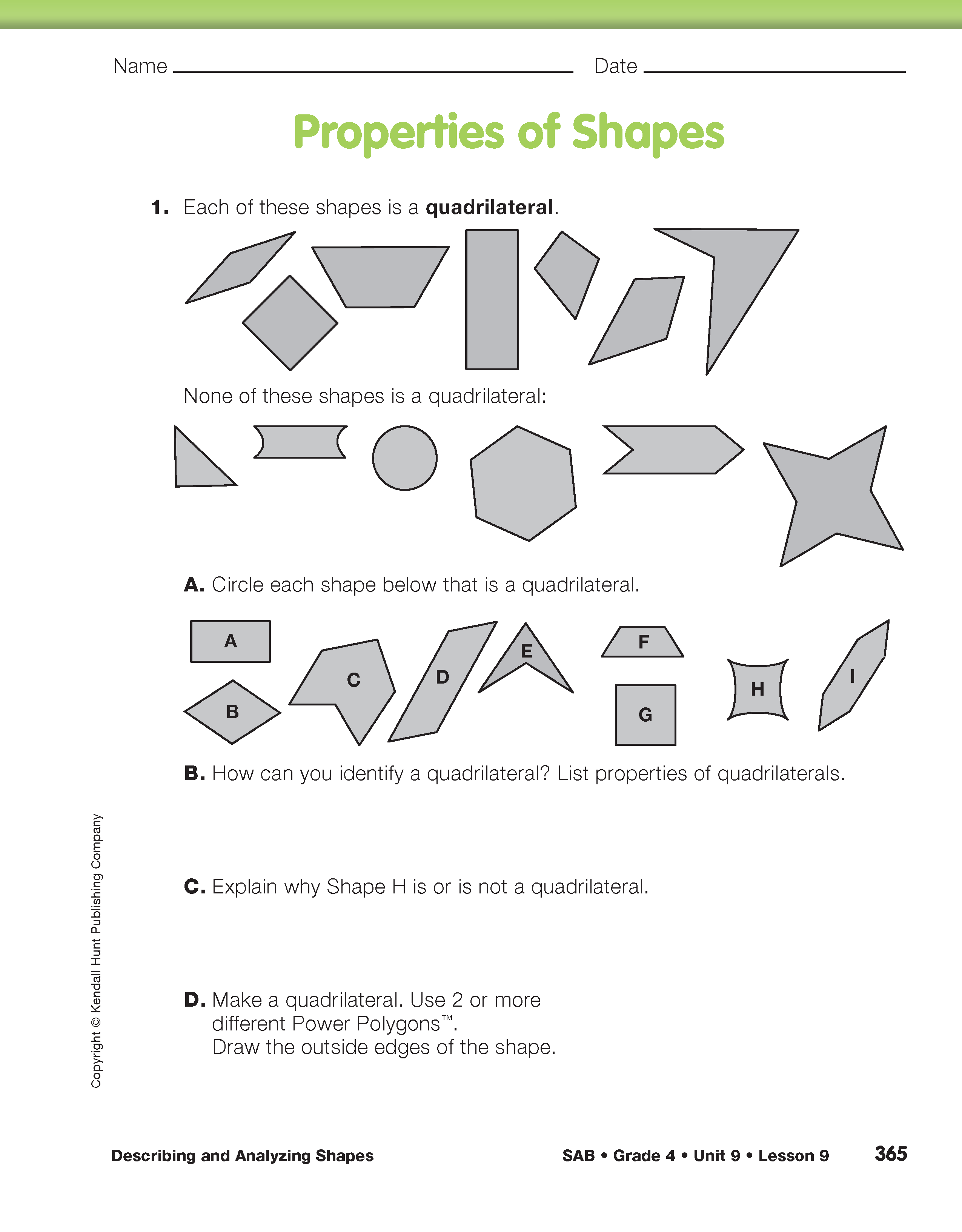
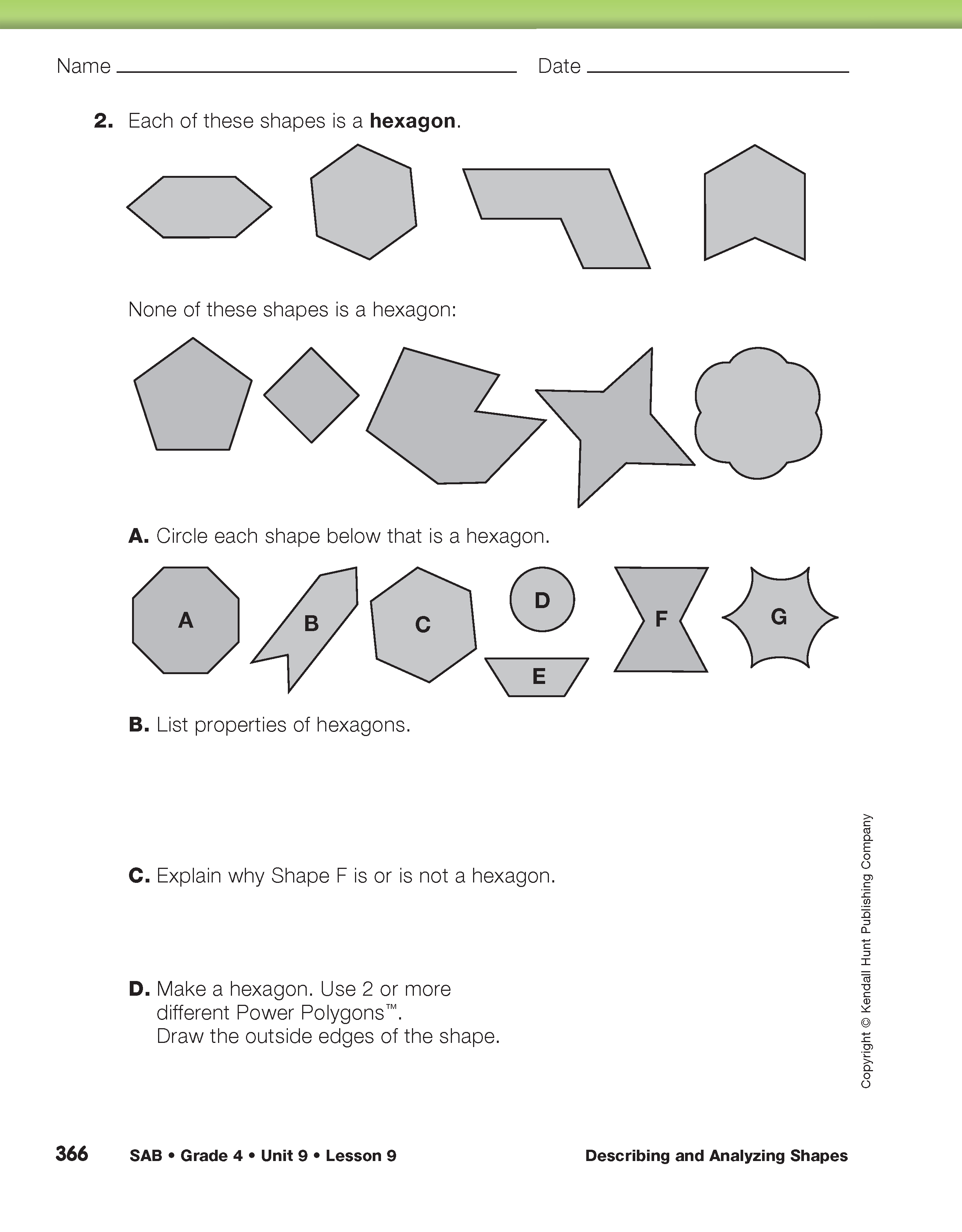
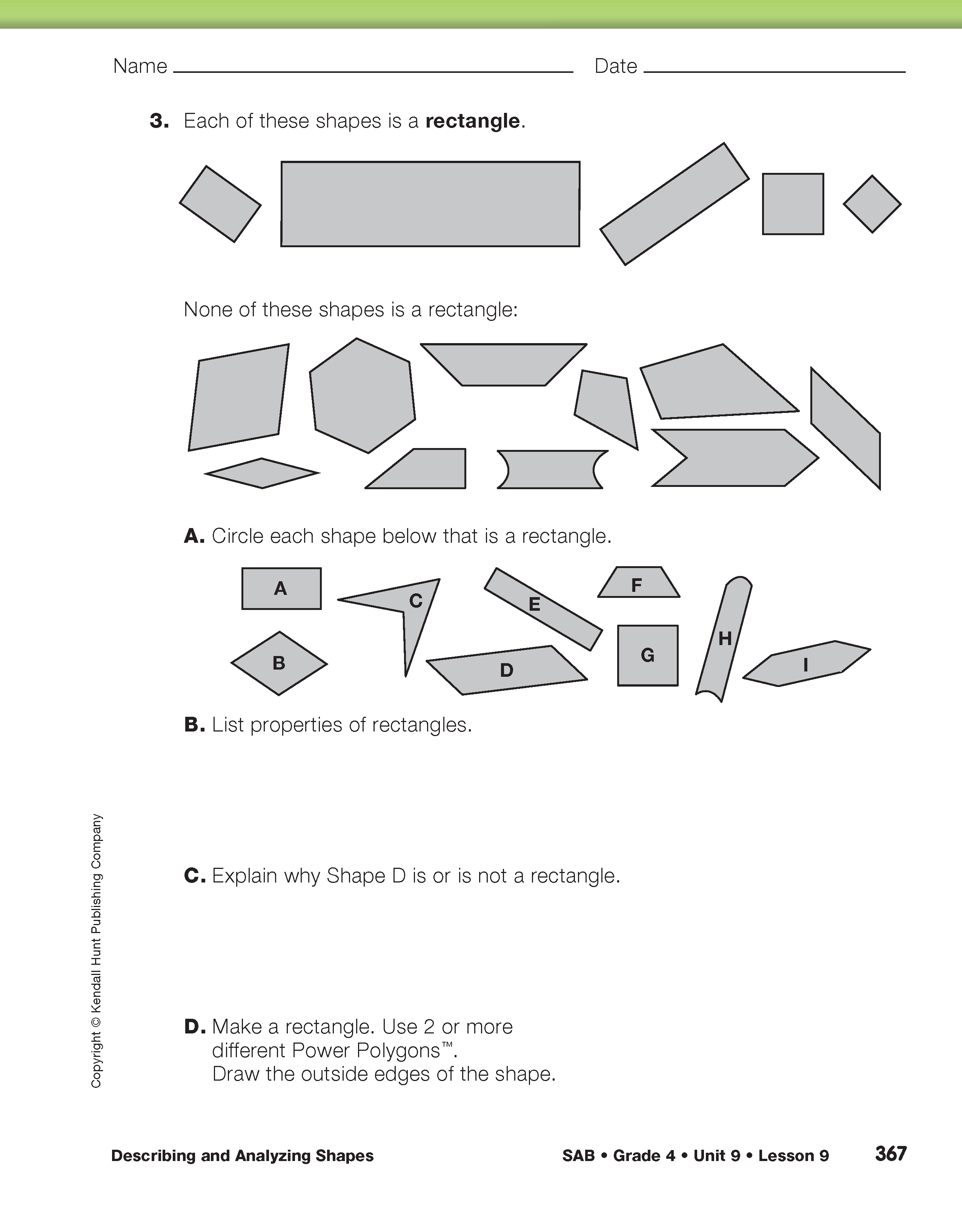
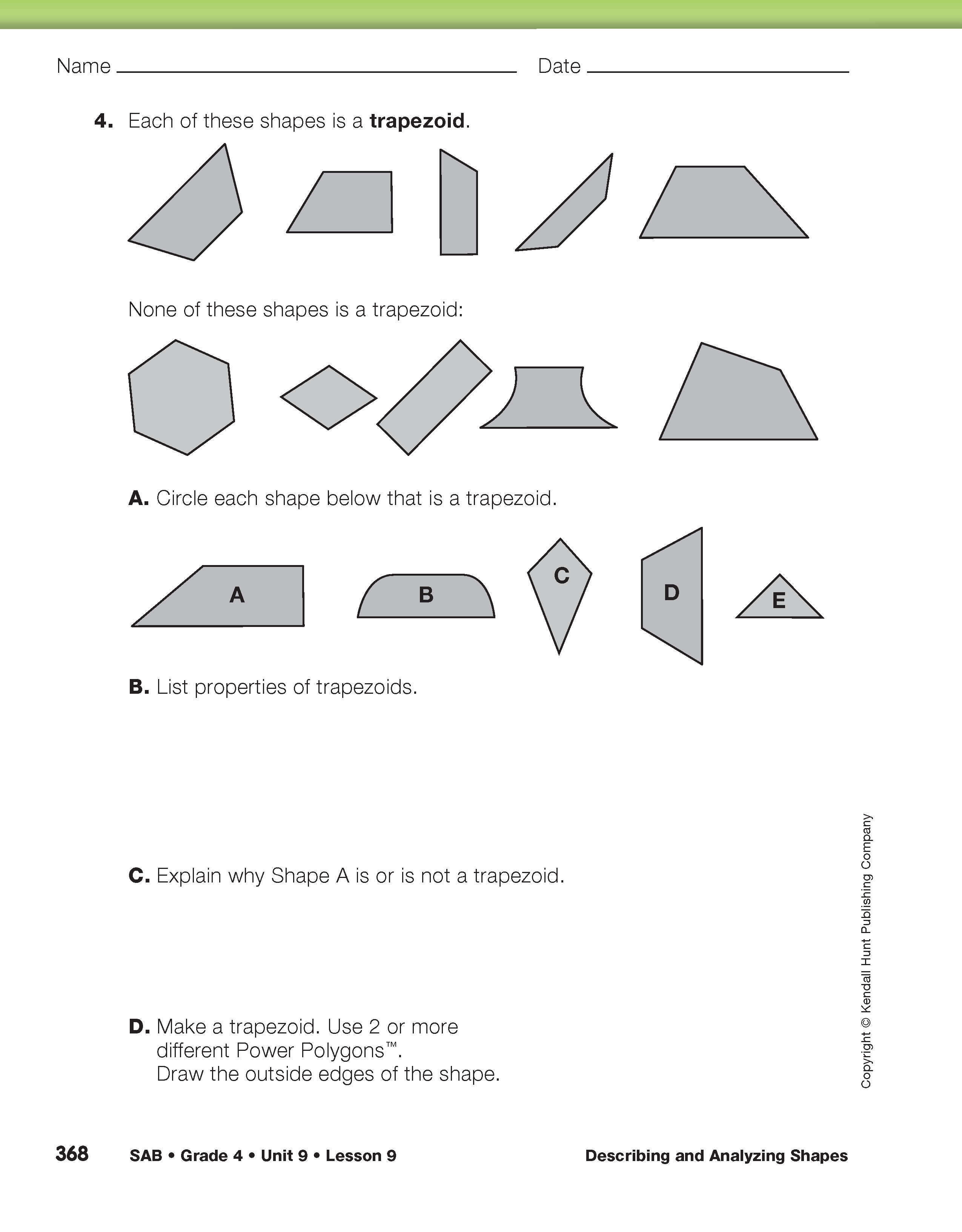
Have partners complete Questions 1–4 on the Properties of Shapes pages in the Student Activity Book. Students analyze and describe quadrilaterals, hexagons, rectangles, and trapezoids using questions similar to those in the Student Guide for parallelograms. As students work, encourage them to use the list of questions in the Student Guide to guide their work.
For example, for the quadrilaterals, ask:
- How many sides does each quadrilateral have? (4)
- Can you say anything about the relationship between the sides? Are any sides parallel? (Some are but they don't have to be.) Is that true for all the quadrilaterals? (No.)
- Is there something the same about the size of the angles in all the quadrilaterals? Is there something the same about the size of the angles in all the quadrilaterals? (No, but they all have 4 angles.)
If time is short, assign each pair of students two shapes to analyze. For example, assign half the class quadrilaterals and rectangles (Questions 1 and 3) and the other half of the class the hexagons and trapezoids (Questions 2 and 4).
When students have completed a list of properties and drawn each shape using Power Polygons™, continue the class discussion of properties using the class charts for each shape. Have volunteers take turns adding properties to each chart (Questions 1B, 2B, 3B, and 4B). See Figure 9. As they add properties, encourage the class to challenge each student to justify the newly added property. If students differ on whether a property is always true, ask the challenger to show an example from the set of shapes that does not have the named property. See the sample dialog.

Use this dialog to discuss properties of the quadrilaterals shown in Question 1 in the Student Activity Book.
Michael: All the quadrilaterals have an acute angle. [He points to the acute angles in the rhombus, trapezoid, kite (third shape from right), and arrow (shape on far right).] Look, all these angles are pointy.
Irma: I don't think so.
Teacher: Show Michael an example of at least one of the quadrilaterals that does not have an acute angle.
Irma: The rectangle doesn't have an acute angle.
Teacher: How do you know?
Irma: It has all right angles, so no acute angles. I can show it with a corner of an orange square.
Have one or two students draw the shapes they made from two or more Power Polygons™ (Questions 1D, 2D, 3D, and 4D). Have the class check to see that the new shape has all the properties listed for that shape on the chart, including number of sides. See Figure 8 for a sample parallelogram.
Use Properties. After students have completed the discussion for Questions 1–4, assign Check-In: Question 5. Students who are confident finding and using properties of shapes can complete all parts of this question independently. Students who still need some support can work with a partner for all or some of the sections of this question.
Observe students as they work and evaluate their written work on rhombuses for Check-In: Question 5 in the Student Activity Book. Document students' abilities to describe and analyze 2-dimensional shapes based on their properties [E5] and justify conclusions using geometric properties [E10].
Targeted practice for these Expectations is in the Workshop in Lesson 11. The Shape Finder game and the Name That Property game can be used as targeted practice.

Definitions. A class of geometric objects can be defined in more than one way. For example, here are three definitions of a parallelogram:
(a) a quadrilateral with two pairs of parallel sides
(b) a quadrilateral with two pairs of parallel and congruent sides
(c) a quadrilateral with both pairs of opposite sides parallel
Each of the above definitions is mathematically correct.Mathematicians prefer minimal definitions, those that are as short as possible. For example, in definition (b) it is not necessary to say that the sides are congruent because it can be proved that if both sets of opposite sides are parallel, the parallel pairs will be the same length. At this point in students' development, it is enough for students to be able to identify properties of shapes. Using and developing rigorous definitions will come in later grades.
Definition of a Trapezoid. Math Trailblazers uses the definition of trapezoid that says that a quadrilateral is a trapezoid if it has exactly one pair of parallel sides. Using this definition, parallelograms are not trapezoids because they have two pairs of parallel sides. Other mathematicians use another common definition that says a quadrilateral is a trapezoid if it has at least one pair of parallel sides. This definition includes parallelograms.
It is important for the class to agree on one definition. It is also interesting to note that not all mathematicians agree on all geometric definitions.