Angles in Polygons

Est. Class Sessions: 3

Developing the Lesson

Part 3. Triangles

Adding the Angles of a Triangle.

Begin a transition to this part of the lesson by asking:

What is the smallest number of sides a polygon can have? (3)
Why can't a polygon have one or two sides? (One possible response is that if a shape were made of two line segments connected to each other at the end points, there would not be any space between the segments to make a shape. The result would be just another line segment.)
What is the name of a polygon with three sides (and three angles)? (triangle)

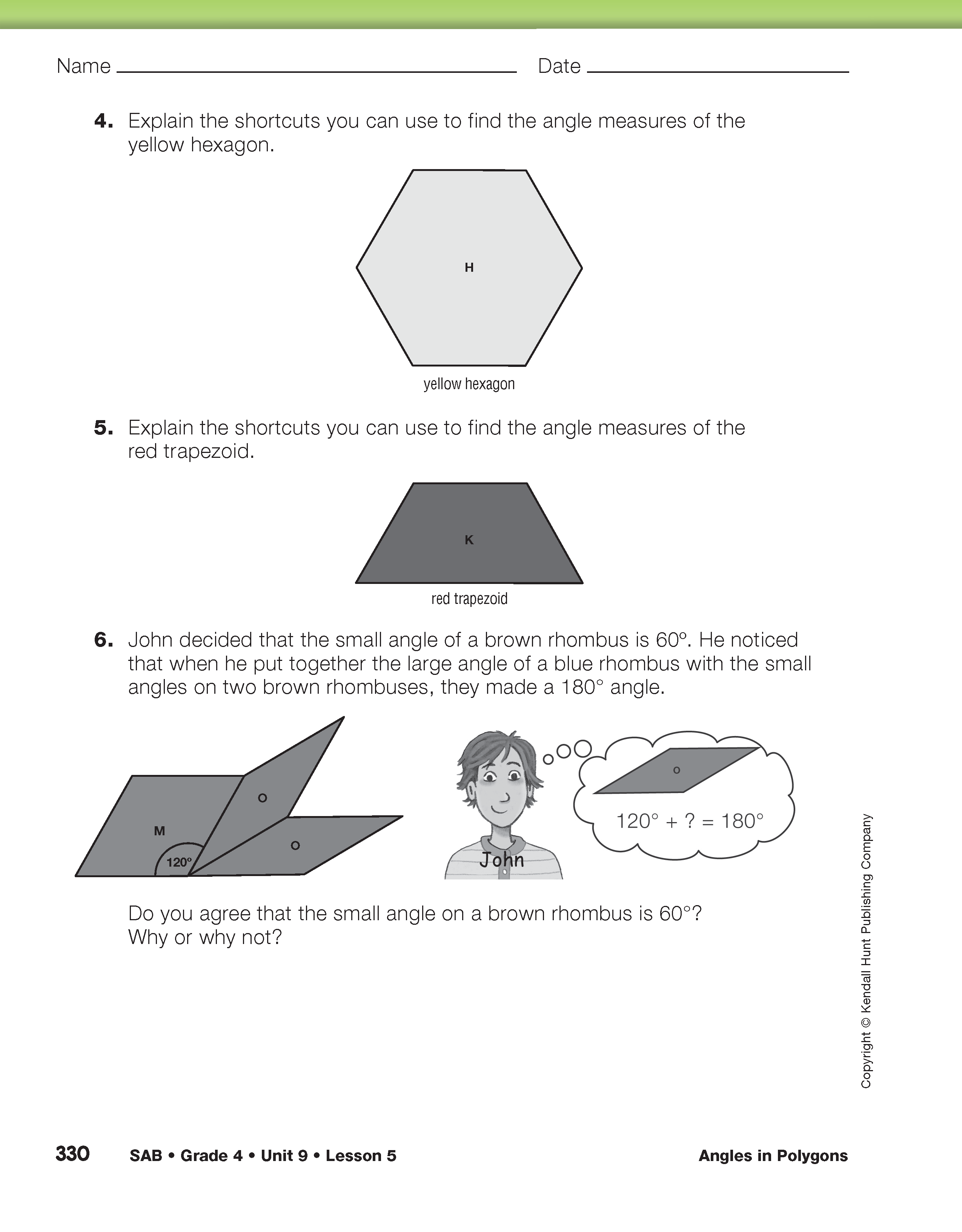
Explain that there are special relationships between the angles on the inside of a polygon. To start investigating these relationships, it will be easiest to look at the triangle.

Direct students to Questions 2–7 in the Adding the Angles of a Triangle section the of Angles in Polygons pages in the Student Guide. Following the directions, students should find that the sum of the angle measures in their triangle is close to 180 degrees, or a straight angle. Students compare their visual inspection of the sum of the angles (Question 6) with their calculated result (Question 7).

Make sure students tear the corner off their triangles, rather than cut them. When the corner is cut, it is harder to tell which angle was a corner of the original triangle. Also make sure students' torn pieces still show the written angle measures.

In Question 8, students compare their results with other students. They should discover a pattern that every triangle measured shares a similar result. Students test this pattern with triangles from their sets of Power Polygons™ and write a rule (Questions 9 and 10). As students discuss and write answers for Question 11, introduce the concept of measurement error. Students may respond that the measurements were different because Romesh and Ana “made mistakes measuring the angles.”

Probe these responses more deeply by asking:

What are some kinds of errors they might have made? (Some possible responses are that they positioned the protractor incorrectly, they misread the protractor measurement, they did not draw extensions to the line segments in the shapes, they drew “crooked” extensions to their line segments, they made mistakes adding, or they did not draw their triangles precisely in the first place.)
How can we make these errors as small as possible? (by being careful to reduce the types of mistakes described above)
Can errors be completely eliminated? (No; measurement always includes some amount of error. The goal is to make errors as small as possible.)

Use Question 12 to lead a class discussion about the combinations of angles that can be found in triangles. Ask students to justify their answers based on their rules about the sum of angles in a triangle. Ask questions similar to those in the Sample Dialog for Question 12C.

Discussion of Question 12C in the Student Guide.

Teacher: Can a triangle have more than one obtuse angle?

Linda: No.

Teacher: Why not?

Linda: Because if you start to draw the triangle with two obtuse angles, you can't make the last two sides meet.[draws line segments as shown in Figure 5]

Teacher: What if you made the angle on the left smaller to begin with?

John: If they're both obtuse, you still wouldn't be able to make the sides meet. The two sides will always get farther apart as you go up, not closer together. [draws line segments as shown in Figure 6]

Teacher: Good. Can you prove the same thing using angle measures?

Tanya: I think so. If two angles are obtuse, that means they are both bigger than 90 degrees. So if you add them together, they have to be more than 180 degrees.

Teacher: And what does that tell you?

Jerome: It tells you it can't be a triangle.

Teacher: Why not?

Jerome: Because all three angles have to add up to 180 degrees. But we already have more than 180 degrees and only two angles. It doesn't work for a triangle.

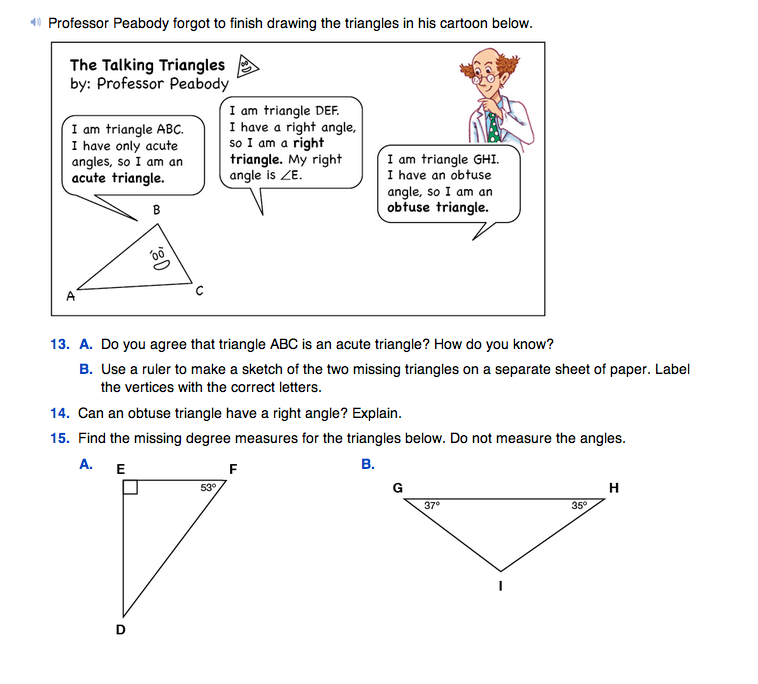
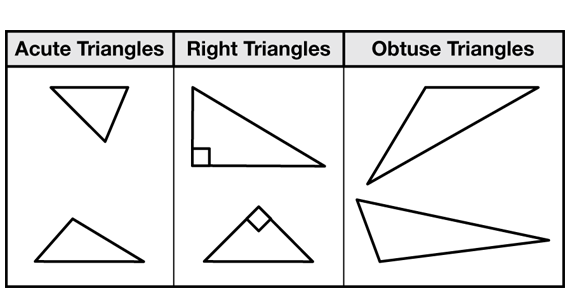
Classify Triangles. In Question 13 in the Student Guide, students are introduced to classifying triangles based on their angles. Figure 7 shows these three types of triangles.

A right triangle has one right angle. An obtuse triangle has one obtuse angle. An acute triangle has three acute angles. Because the three angles of a triangle sum to 180°, two of the angles must always be acute in any triangle. We can therefore think of these triangle categories in terms of the third angle of the triangle, which can be either acute, right, or obtuse.

Question 13B is most students' first opportunity to draw triangles in this unit. Help students with this task with a few reminders.

Use a ruler to draw the line segments.
Make sure the ends of their line segments touch, but do not cross.
Draw a light sketch to show the angles and sides correctly before retracing the triangle more boldly.
Check angle sizes by comparing them to a right angle.
Label the vertex points with letters.

In Question 14, students use what they have learned about the sums of angles in triangles to again reason about the combinations of angles in a triangle. An obtuse triangle cannot have a right angle because the sum of the obtuse angle and a right angle already exceed 180°.

Find the Missing Angle. Have students work with partners to solve the problems in Question 15. Students apply the rule about triangle sums to find the missing measures of angles in a triangle. Introduce these problems with the whole class to help students engage with the mathematics.

Ask:

For Question 15A, what does the question ask you to find? (The measure of ∠D)
What do you already know? (∠F is 53° and ∠E is 90°.)
What else do you know about the angles of a triangle from the activity you did earlier? (All three angles add up to 180°.)
Can you use your protractor to measure any of the angles? (The instructions say, “Do not measure the angles.”)
How will you be able to tell if your answers are reasonable? (Estimate the angle size as a check. For example, look at the picture and ask yourself if ∠D should be greater than or less than 90 degrees?)
What questions do you still have about what the problem is asking?

From this point, allow students to develop their own solution paths to find the missing angle. Students may use flexible strategies to represent and solve the computation. After students have found solutions to both problems, select a few students to share their strategies with the whole class.

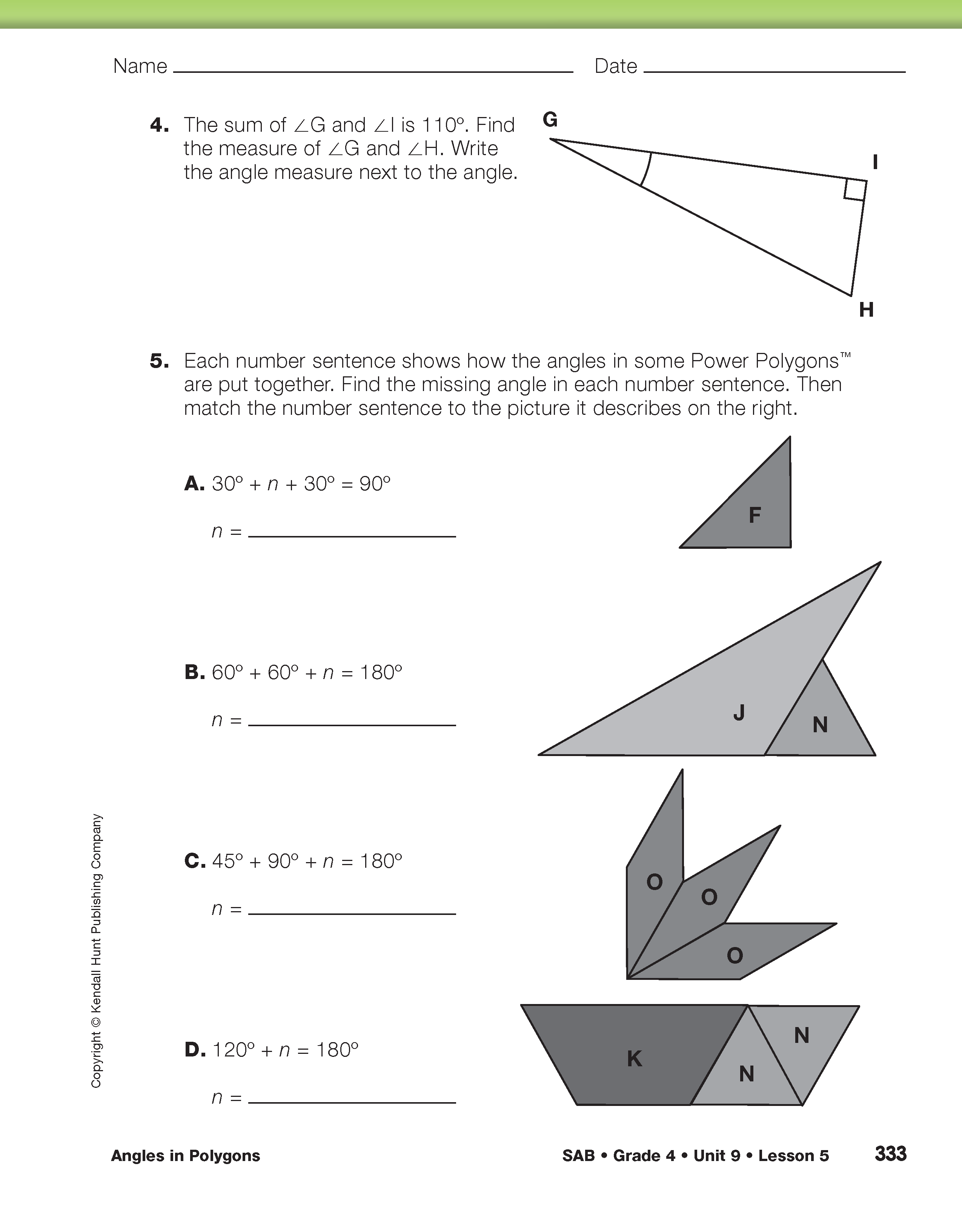
After students have shared their solutions, challenge student pairs to find the missing angles in the triangle in Question 16. Students should use what they know about the sum of the angles of a triangle and that a straight angle is 180°.

Add and Subtract Angles. Refer students to the Add and Subtract Angles pages in the Student Activity Book. Ask them to work with a partner to complete and discuss the questions on these pages. Students will need a protractor for Question 1. When students are done, ask students to share their solutions to Questions 2–5. Question 5 asks students to connect number sentences to how angles are put together. A display of this page may help discuss the representations in this question.

Assign Questions 5–8 in the Homework section of the Student Guide.